ALT阅读笔记
什么是数据布局优化
数据布局优化旨在通过重写张量数据的存储格式,以减轻访问内存的开销。因此,数据布局优化通常被归类为图级优化。存储格式指的是张量维度的排列方式。以二维卷积(C2D)算子为例,C2D的输出张量的流行数据布局包括NOHW、NHWO和NWOH几种,其中N、O、H、W分别表示批量大小、输出通道数、输出张量的高度和宽度。在GPU上广泛使用HOHW,在TensorFlow中,默认布局是NHWO,而HWON则在数字信号处理中使用。
概览
关于数据布局优化的2个观察:
观察1:联合进行数据布局优化和循环优化是有益的。我们通过一个实验来说明这一点,该实验分别基于𝑁𝑂𝐻𝑊、𝑁𝐻𝑊𝑂和𝐻𝑊𝑂𝑁布局优化C2D的循环。我们的平台包括32核的Intel Xeon Silver 4110 CPU@2.1GHz、NVIDIA RTX 2080Ti GPU和麒麟990 ARM SoC。我们在图1中报告了性能,其中延迟轴是对数刻度,每个硬件涉及多个运算符配置(不同的通道数量、卷积步长等),以覆盖丰富的工作负载。我们观察到,最佳布局可以分别在Intel CPU、NVIDIA GPU和ARM CPU上平均提高循环优化性能的55.9%、87.2%和48.8%。相反,当没有来自循环优化的反馈时,选择不同布局并不容易,因为算子设置和平台的特性的差异非常大。
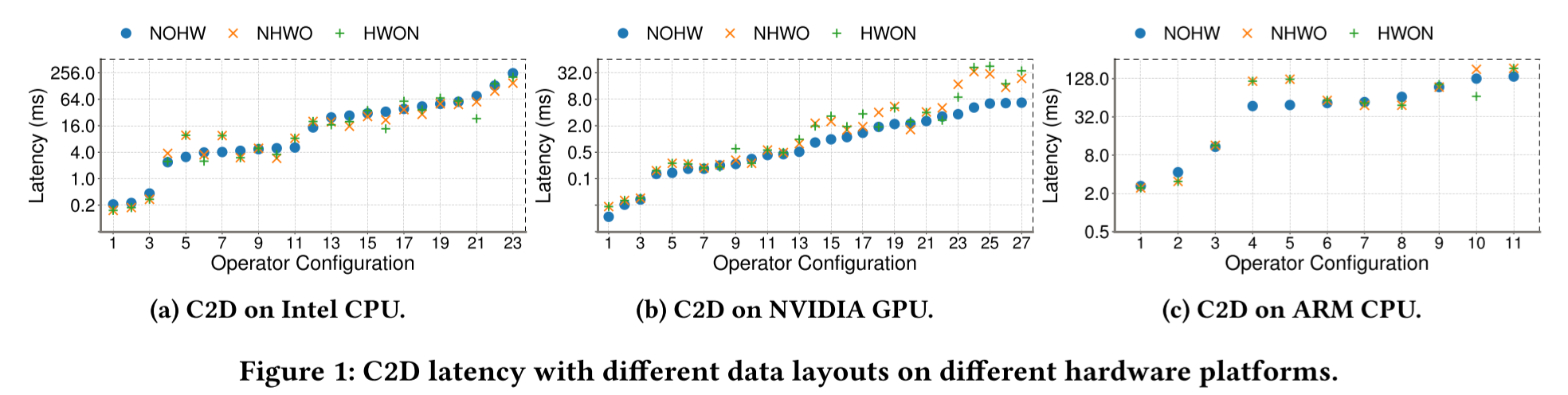
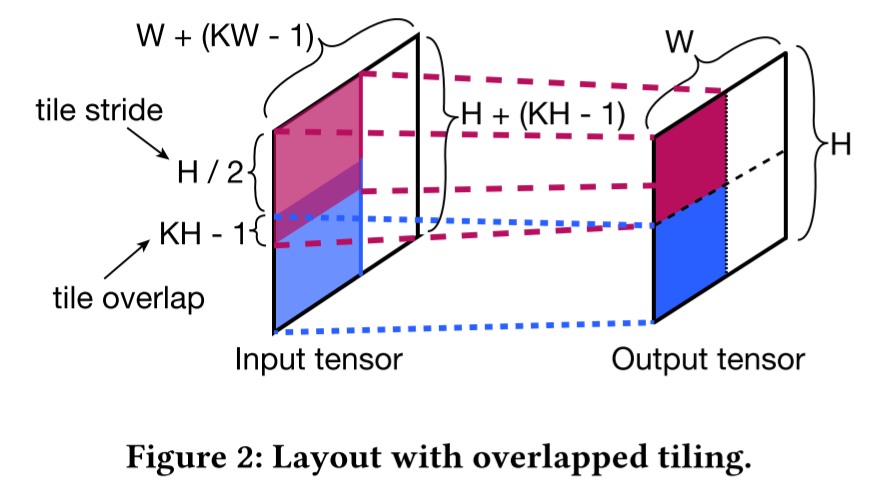
观察2:由于布局操作的高成本,现有解决方案无法有效进行联合调优。现有系统通常将张量存储与算子的实现耦合在一起,因此更改布局需要重新实现。这种高昂的布局操作成本限制了可以探索的布局选择数量,并进一步导致单向的优化流程。以$N\frac H {H_t} \frac W {W_t} \frac O {O_t}H_tW_tO_t$布局为例,这个布局超出了常见的$NOHWO_t$布局的调优空间,很难在没有联合调优的情况下手动或自动发现。它可以实现比$N\frac O {O_t}HWO_t$快32.4%的性能改进。除了在通道维度上进行平铺外,该布局还将输出张量的空间维度(高度和宽度)进行分块,当$H_t$和$W_t$都为2时,相当于将空间分为了4块。输出张量的每个空间块具有形状$\frac H 2 × \frac W 2$ 。对于具有卷积步幅1的C2D,输入张量的高度和宽度为 𝐻 + (𝐾𝐻 −1) 和 𝑊 + (𝐾𝑊 −1),其中 𝐾𝐻 和 𝐾𝑊 是卷积窗口的高度和宽度。由于C2D的滑动窗口操作具有自然的重叠,每个输出块需要一个与卷积相关的输入张量的平铺。这导致了图2中的布局,其中每个彩色区域表示一个平铺块,沿着输入张量高度的平铺块之间的重叠恰好为 (𝐾𝐻 − 1)。这种带有重叠的多维平铺促进了数据局部性和缓存利用,但给数据布局变化带来了挑战。
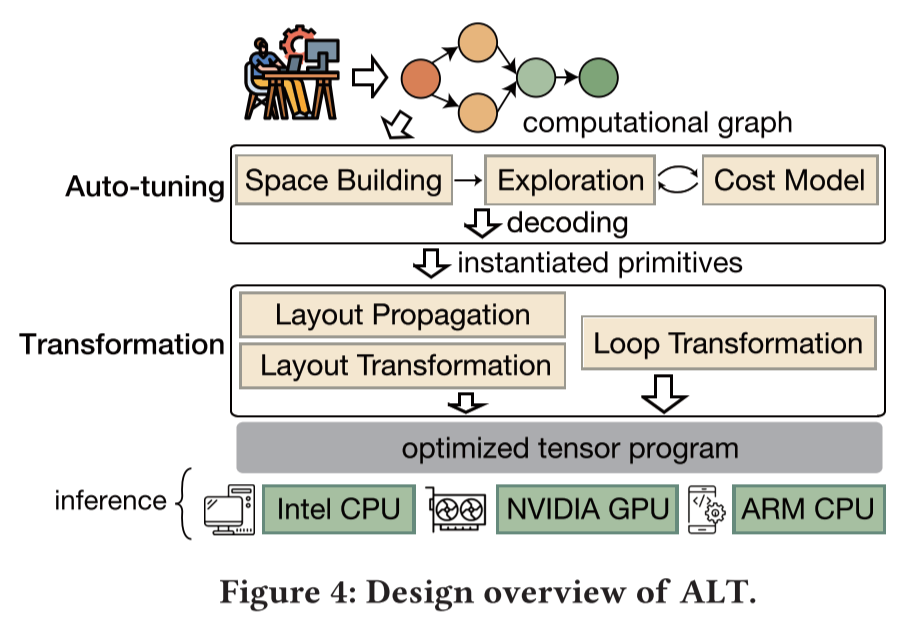
ALT的系统概述如图4所示,它包括两个主要模块:自动调优和转换。转换模块是一个通用基础设施,通过易于使用的原始函数实现低成本的布局和循环操作。基于此,自动调优模块通过在原始函数的参数空间中搜索来执行数据布局和循环优化。ALT的工作流程如下:首先,用户提供一个深度模型的计算图,可以使用特定领域语言(例如Python的子集)来表示,也可以从其他框架(例如TensorFlow)生成的模型文件构建。其次,自动调优模块建立张量和操作符的搜索空间,并共同探索该空间。为了减少调优时间,它使用成本模型来最小化耗时的设备测量。当探索完成时,它将在空间中找到的最佳性能点解码为一系列布局和循环原语,并将这些原语传递给转换模块。第三,布局传播子模块传播布局原语。然后,转换模块应用所有原语执行布局和循环转换,生成优化的张量程序。最后,我们将程序部署到不同的硬件上进行推断。
布局转换原语
为了实现低成本的布局操作和简化布局调整,ALT设计了各种原始函数来转换数据布局:split、reorder、merge、unfold、pad和store_at。其中,split、reorder和fuse是基本的原始函数,其他函数则属于高级原始函数。
基本原语:执行一对一的转换。例如,假如想将$NOHW$布局转换为$N\frac O {O_t}HWO_t$布局,我们需要这样做:
split(T, dim=2, factors=[O // o_t, o_t])
reorder(T, perm=[1, 2, 4, 5, 3])
高级布局原语:上述示例展示了基本原语的多功能性。然而,有些情况无法涵盖,例如图2中的重叠平铺。为了实现这样的特殊变换,我们引入了高级布局原语:展开(unfold)、填充(pad)和存储(store_at)。
unfold:这个基元执行重叠平铺。它接受一个tile_size参数和一个stride参数,其中stride是两个平铺之间的间隔。例如,一个数组 {1, 2, 3, 4, 5} 可以通过设置 𝐵 = 3 和 𝑆 = 2 来展开为一个二维数组 {{1, 2, 3}, {3, 4, 5}}。unfold对于滑动窗口的计算模式非常有用,例如卷积层。
除了展开操作,我们还提出了填充(pad)和存储位置(store_at)的原语。填充原语是为所选维度添加零值,这对于在NVIDIA GPU的共享内存上对齐数据并减轻存储器冲突非常有用。存储位置原语允许将两个张量融合在一起,通过将一个张量附加到另一个张量上来提高张量间的数据局部性。例如,在全连接层中,它可以将偏置向量的每个元素附加到权重矩阵的每一列上。随后,在常规矩阵乘法(GMM)中,可以通过访问同一缓存行中的权重列和偏置元素来同时计算内积和偏置相加操作
布局转换原语可能会产生开销。具体而言,我们发现了两种这样的开销:布局转换开销和融合冲突开销。
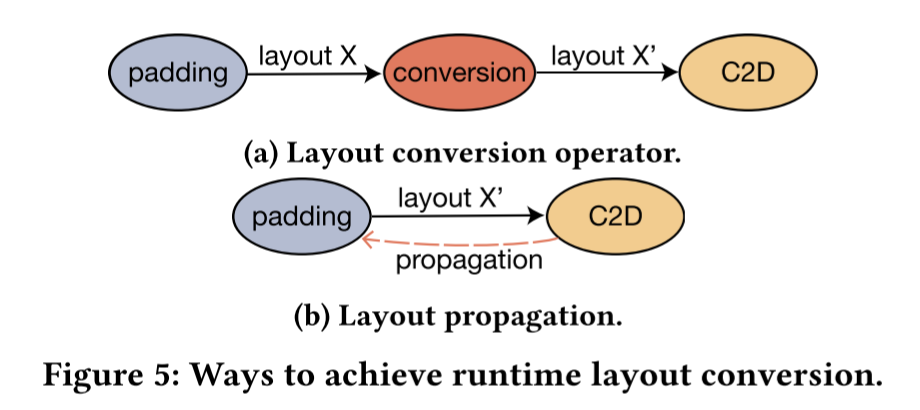
布局转换开销来自于如下情形:假如C2D的输入为前一个算子的输出,而这个算子的输出布局与C2D不匹配,那么我们就要在中间插入一个布局转换算子,带来额外的开销,如图5所示。因此,ALT采用布局传播的方法。在传播之后,padding运算符实际上在运行时执行两个任务:填充零和转换布局。
运算符融合是一种循环调优技术,通过让下游运算符在缓存溢出之前立即使用中间数据来促进运算符间的数据局部性。图6展示了一个C2D算子紧接着一个relu算子。由于布局的转换,C2D的循环嵌套被相应地重构,导致无法与relu融合。

为了消除由布局转换引起的融合冲突开销,我们扩展了布局传播机制,使得多个张量可以共享相同的布局。布局传播可以通过复制源张量的原始布局转换序列到目标张量来实现。例如,在图6中,我们复制了张量𝐶𝑜𝑛𝑣的原语序列,即分割和重新排序的原语,用于张量𝑅𝑒𝐿𝑈。然后,ReLU将触发相同的循环嵌套重构,从而与C2D完全对齐。结果如图7所示。

尽管布局传播有助于消除布局转换所带来的开销,但它有三个限制。首先,我们只会沿着仅包含逐元素操作符的路径以及形状相同的张量之间传播原语。其次,如果原语序列包含高级原语,我们将不会进行传播。这是因为高级原语会导致数据扩展。相反,当出现这种情况时,我们会插入转换操作符。第三,每个复杂操作符的布局调整将独立进行。
循环变换原语
我们通过重复使用 TVM 的循环原语来进行循环转换:分割(split)、重新排序(与布局名称相同,但功能不同)、向量化(vectorize)、展开(unroll)、缓存读写(cache_read/write)、并行化(parallel)、内联(inline)和计算位置(compute_at)。大多数循环调优技术,包括循环切片、向量化和操作融合,都可以通过组合这些原语来实现。
自动调优
我们的联合调优包括三个步骤:1)为张量构建布局调优空间,并为运算符构建循环调优空间,空间中的每个点可以解码为原始序列;2)探索调优空间,找到最佳性能点;3)将该点解码为实例化的原语,并将其传递给转换模块。
调优空间构建
通过我们的转换模块,我们只需要找到应用原语的最佳参数。因此,调优空间等同于原语的参数空间。目前,我们只考虑布局空间中的布局分割、重新排序和展开原语。
我们需要对要构建的布局空间进行修剪,否则它将是无限大的,因为可以应用的原语数量是无限的。正如在第1节中所述,我们只对复杂运算符进行布局调优,并将其结果传播以减少调优任务的数量。此外,我们为每个由复杂运算符访问的张量设计了一个布局调优模板。每个模板只公开一部分原语参数作为可调优选项。
因此,我们的布局调优模板是一个平铺(tiling)模板,其中平铺大小作为基本可调选项。对于大多数维度,可以使用分割原语实现平铺。对于卷积的高度和宽度维度,可以使用展开原语实现重叠平铺。在进行分割和展开之后,基于第一个观察结果,我们将平铺的通道维度设置为最后一个维度,以促进数据重用和SIMD。因此,我们用于C2D的数据布局调优模板具有以下形式:

对于矩阵乘法GMM$C = A \times B$,我们这样进行变换:
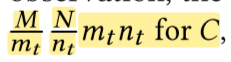
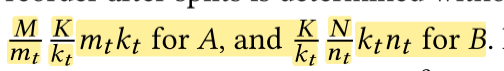
上述模板仅执行一级多维布局平铺。我们可以轻松将它们扩展到多级情况。
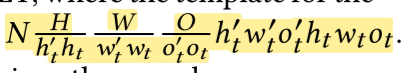
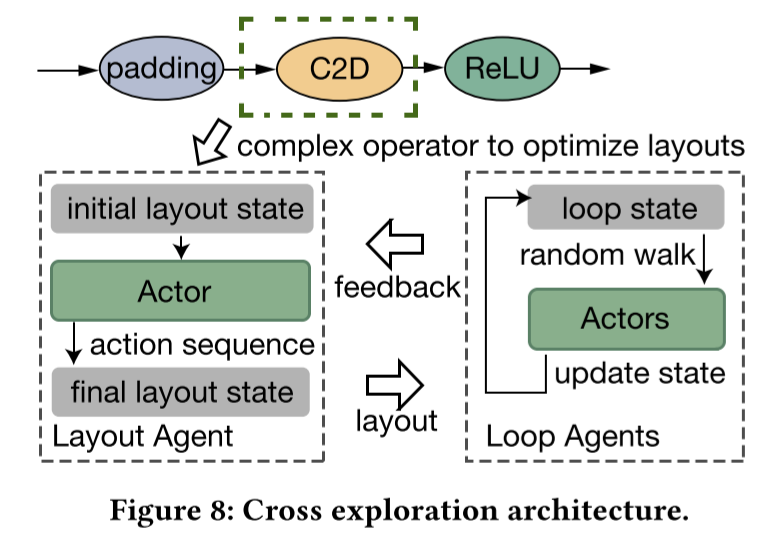
探索调优空间
采用强化学习的PPO算法
测试

定义了ALT的两个变体:(1) ALT-OL,仅使用循环优化;(2) ALT-WP,仅消除复杂算子之前的转换操作(即如图5(b)所示的基本布局传播)。与Ansor相比,ALT在Intel CPU、NVIDIA GPU和ARM CPU上分别实现了1.47倍、1.39倍和1.46倍的加速。对于R3D,大多数运算符都是计算密集型的,因此ALT与Ansor的结果相似。对于MV2,这是一个计算强度较低的轻量级网络,ALT明显优于基准方法。
请注意,ALT-OL与Ansor的性能相似,因为它们两者主要涉及循环调优。当结合布局调优和基本布局传播时,ALT-WP通常比ALT-OL快1.1倍,并在少数情况下没有改进。与ALT-WP相比,ALT的平均加速比为1.3倍。这是因为运算符融合是一种关键的循环调优技术,可以提高性能,而ALT-WP不能有效地结合布局调优和循环调优。