Basic Math
1 Some notations
- \(\mathbb{R}[X]\) :多项式集合,其多项式的所有系数(coefficients)都在\(\mathbb{R}\)中。例如,\(\mathbb{Z}[X]\)代表所有系数为整数的多项式。
- \(\mathbb{Z}_a[x]/(x^n +1)\): 系数为\(\{\lceil - \frac{a}{2} \rceil , \dots, \lfloor \frac{a}{2} \rfloor\}\),不超过\(n\)阶的多项式。
2 商环(The Quotient Ring)
商环 \(\mathbb{C}[X]/(X^N +1)\) 是通过将多项式 \(\mathbb{C}[X]\) 模 \(X^N +1\).
例子: \(\mathbb{C}[X]/(X^3 -1)\):
\(\mathit{p}(X) = X^4 + 2X^2 +3\). 模 \(X^3 -1\):
\[X^4 \equiv X \cdot X^3 \equiv X \cdot 1 = X.\]因此, \(\mathit{p}(X) = X + 2X^2 +3\).
商环主要作用是构建一个有限域,其在后续的典范嵌入中也起到重要作用。
3 N次单元根(The N-th roots of Unity)
N次单位根是以下方程的复数解:
这些根的解为:
\[\omega = e^{2\pi ik/N}, k = 0,1,2,...,N-1\]其中, \(\left\{\omega = e^{2\pi ik/n} \mid \gcd(k, n) = 1\right\}\) 是 本原N次根。因为只有当 \(\omega\) 为n次方时才等于1,即\(\omega^n =1\) ,也称之为阶为n的单元根。
4 RLWE问题
一个加密方案通常会基于一个困难问题来设计,而LWE问题就是同态加密方案里的常用困难问题。
LWE(Learning with Errors)问题:
- 给定一个随机矩阵 \(A \in \mathbb{Z}_q^{n \times m}\) ,一个秘密向量 \(\mathbf{s} \in \mathbb{Z}_q^n\),以及一个“噪声”向量 \(\mathbf{e}\),目标是通过观测 \((A, \mathbf{b} = A\mathbf{s} + \mathbf{e} \mod q)\) 来恢复 \(\mathbf{s}\)。
- 噪声 \(\mathbf{e}\) 通常来自某个已知的概率分布(如离散高斯分布)。 由于噪声的加入,恢复 \(\mathbf{s}\) 是极其困难的。
RLWE(Ring Learning with Errors) 是LWE问题的一个重要变体,通过将LWE问题的矩阵运算结构化为多项式环上的运算,显著提高了效率,同时保留了其计算难度和安全性。 典型的环定义为:
- \(R = \mathbb{Z}[x] / (f(x))\),其中 \(f(x)\) 是一个不可约多项式(通常为 \(x^n + 1\),且 \(n\) 是2的幂)。
- 元素定义在模数 \(q\) 的有限域上,即 \(R_q = \mathbb{Z}_q[x] / (f(x))\)。 给定:
- 一个公开的多项式 \(a(x) \in R_q\);
- 一个秘密多项式 \(s(x) \in R_q\);
- 一个误差多项式 \(e(x) \in R\)(通常取自某个离散高斯分布或均匀分布); 计算: \(b(x) = a(x) \cdot s(x) + e(x) \pmod{q}.\) 目标是从 \((a(x), b(x))\) 中恢复秘密多项式 \(s(x)\)。
RLWE中的多项式乘法可以用快速傅里叶变换(FFT)实现复杂度为\(O(nlog^n)\)的算法,而LWE中的矩阵运算复杂度为\(O(n^2)\)。
5 典范嵌入
典范嵌入(Canonical embedding)是一种将多项式转为向量的方法。
给定多项式 \(a(x) \in \mathbb{Z}[x] / (f(x))\),其 Canonical Embedding 的定义如下:
\[\Phi(a(x)) = (\sigma_1(a(x)), \sigma_2(a(x)), \dots, \sigma_n(a(x)))\]其中 \(\sigma_i\) 表示将 \(x\) 替换为 \(f(x)\) 的第 \(i\) 个根 \(\alpha_i\),即:
\[\sigma_i(a(x)) = a(\alpha_i).\]这里 \(\alpha_i\) 是 \(f(x)\) 在复数域中的根。所以Canonical Embedding 的定义可简化为:
\[\Phi(a(x)) = (a(\alpha_1), a(\alpha_2), \dots, a(\alpha_n))\]示例: 输入:
- 定义多项式 \(f(x) = x^3 - x - 1\)(不可约)。
- 被嵌入的多项式 \(a(x) = 2x^2 + 3x + 5\)。
过程:
- 求根: \(f(x)\) 的三个根为 \(\alpha_1, \alpha_2, \alpha_3\)。例如:\(\alpha_1 \approx 1.32, \quad \alpha_2 \approx -0.66 + 0.56i, \quad \alpha_3 \approx -0.66 - 0.56i\)
- 计算嵌入值: 对 \(a(x) = 2x^2 + 3x + 5\),依次计算: \(a(\alpha_1) = 2\alpha_1^2 + 3\alpha_1 + 5\) \(a(\alpha_2) = 2\alpha_2^2 + 3\alpha_2 + 5\) \(a(\alpha_3) = 2\alpha_3^2 + 3\alpha_3 + 5\) 代入根的值后,得到三个复数结果。
- 构造向量: 嵌入向量为: \(\Phi(a(x)) = (a(\alpha_1), a(\alpha_2), a(\alpha_3))\)
输出:
- 嵌入向量(近似值): \(\Phi(a(x)) \approx (11.56, 8.34 + 4.72i, 8.34 - 4.72i).\)
最终多项式 \(a(x) = 2x^2 + 3x + 5\) 可以用 \(\Phi(a(x)) \approx (11.56, 8.34 + 4.72i, 8.34 - 4.72i)\) 表示。 如果我们将 \(a(x) \in \mathbb{Z}[x] / (f(x))\) 中的 \(f(x)\) 表示为\(x^N =1\), 那么它的根就为n次单元根\(\omega = e^{2\pi ik/N}\),其典范嵌入就是将n次单元根带入到\(a(x)\)中进行求解出长度为n的向量。
6 圆分多项式
6.1 圆分多项式的定义
圆分多项式(cyclotomic polynomial)是一种特殊的多项式,它的根将圆等分。其定义如下:
\[\Phi_n(x) = \prod_{\substack{1 \leq k \leq n \\ \gcd(k, n) = 1}} \left(x - e^{2\pi i k / n}\right)\]\(\Phi_n(x)\) 是整系数多项式,在有理数域中\(\mathbb{Q}\)中不可约(可理解为多项式中的“质数”),它具备以下的递归关系:
\[x^n - 1 = \prod_{d \mid n} \Phi_d(x)\]那么\(\Phi_n(x) = \frac{x^n - 1}{\prod_{d \mid n, \, d < n} \Phi_d(x)}\) 。
例子:
- \(\Phi_1(x) = x - 1\), 因为 \((x^1 - 1)\) 的根是 \(1\).
- \(\Phi_2(x) = x + 1\), 因为\(x^2 - 1 = (x - 1)(x + 1) = \Phi_1(x)\Phi_2(x)\).
- \(\Phi_3(x) = x^2 + x + 1\), 因为\(\Phi_3(x) = \frac{x^3-1}{\Phi_1(x)}\).
- \(\Phi_6(x) = x^2 - x + 1\), 因为\(\Phi_6(x) = \frac{x^6-1}{\Phi_1(x)\Phi_2(x)\Phi_3(x)}\).
根据定义,我们可以知道圆分多项式的根是是 n-次单位根中的那些指数 \(k\) 满足 \(\gcd(k, n) = 1\)。也就是我们之前提到的本原n次根 \(\left\{\omega = e^{2\pi ik/n} \mid \gcd(k, n) = 1\right\}\)。
它的几何含义可以理解为在单位圆上选出本原单位根,并通过这些根构造一个最低次的整系数多项式。
6.2 根的共轭性
根据代数基本定理,多项式的系数为实数时,其复根必须成共轭对出现。这是因为实系数多项式 \(f(x)\) 满足:\(f(z) = 0 \implies f(\overline{z}) = 0\)。
所以,圆分多项式的根成共轭对出现。圆分多项式从 \((x^n - 1)\) 中去掉低次因子得到,因此其根是所有 n-次单位根中与低次约数无关的部分。这些根是本原单位根,必然包含成对的复共轭,因为:\(e^{2\pi ik/n},e^{-2\pi ik/n}\) 总是一起出现在\(\Phi_n(x)\)的根集合中。
例如,\(\Phi_3(x) = x^2 +x+1\)。 它的根是\(e^{2\pi i/3}\) 和\(e^{4\pi i/3}\):
- \[e^{2\pi i/3}= -\frac{1}{2} + i\frac{\sqrt{3}}{2}\]
- \[e^{4\pi i/3}= -\frac{1}{2} - i\frac{\sqrt{3}}{2}\]
6.3 二次幂阶圆分多项式
二次幂阶圆分多项式(power-of-two degree cyclotomic polynomials)是圆分多项式中较为独特的多项式,其定义如下:
\[\Phi_{2^k}(x) = \frac{x^{2^k}-1}{x^{2^{k-1}}-1}\]它的性质如下:
- \[\deg(\Phi_{2^k}(x)) = \varphi(2^k) = 2^{k-1}\]
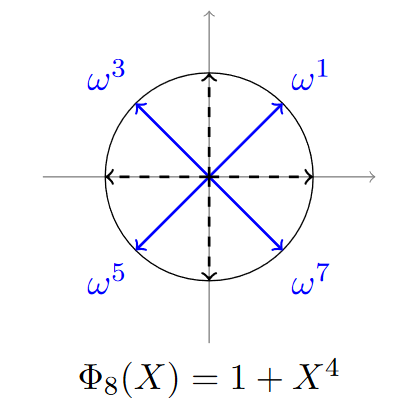
- 它的根为:\(\omega = e^{2\pi i / 2^k}, \, \omega^3, \, \omega^5, \dots, \omega^{2^k-1}\) ,其指数为小于\(2^k\)的奇数
- 它可简化为\(\Phi_{2^k}(x)=x^{2^{k-1}} +1\)
例子:
- \[\Phi_2(x) = x + 1\]
- \[\Phi_4(x) = x^2 + 1\]
- \[\Phi_8(x) = x^4 + 1\]
7 典范嵌入 in 二次幂阶圆分多项式
在 Canonical Embedding 中,多项式的根被映射到复数空间:
- 每个根 \(z_k\) 都会被作为一个数据点;
- 根的复共轭 \(\bar{z_k}\) 必然是同一多项式的另一根。
由于二次幂阶圆分多项式的根成共轭出现,那么只有一半的根是独立的,另一半只是它们的镜像。所以在 Canonical Embedding 中,我们只需要取独立的根即可。
取独立的根可以通过取根的半区间来实现。例如当 \(n = 3\) 时,\(\Phi_8(x) = x^4 + 1\),根为:\(\omega^1, \, \omega^3, \, \omega^5, \, \omega^7\)。我们只需选取 \(\omega^1, \omega^3\) 对应 \(k = 1, 3\),因为 \(\omega^5\) 和 \(\omega^7\) 是它们的共轭。
在群论中,我们可以通过乘法子群\(\{\pm 1\}\) 来实现取根的半区间,它将根分为正方向(独立根),负方向(共轭根)两部分。几何直观上理解:它只取了圆的上半部分,下半部分可以看作上半部分的自然投影。