SpMMPlu阅读笔记
DAC 2023
一句话总结:提出了Sparse IR,用于描述稀疏矩阵乘法(SpMM)在GPGPU和其他硬件上的计算行为;引入了一个名为SpMMPlu的插件,通过3个Pass实现了包含SpMM的计算图的自动编译。
流程概览:
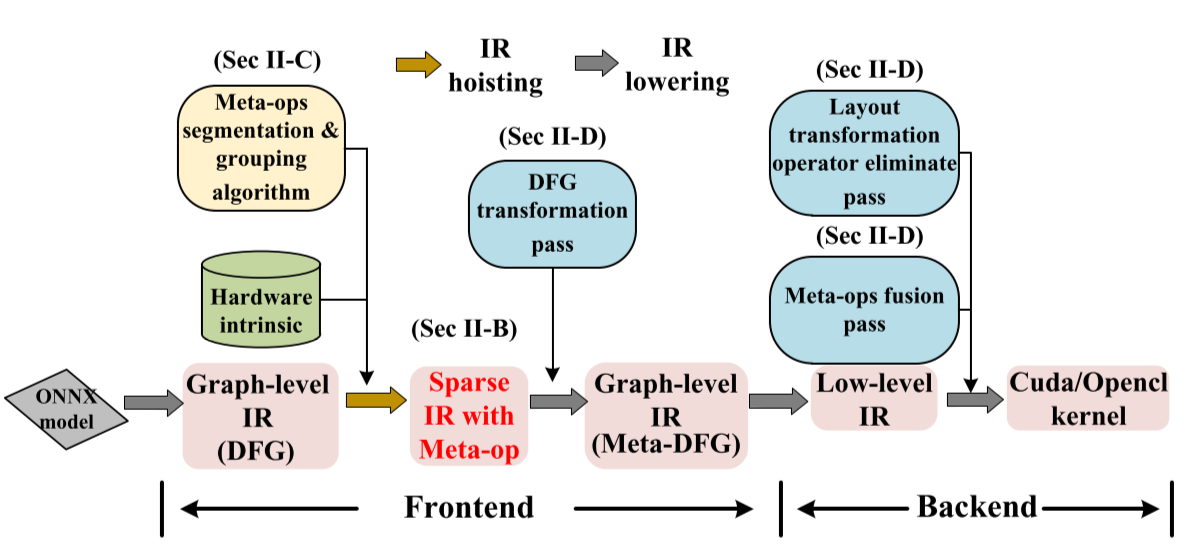
首先将输入的ONNX模型下降为图级别的IR,即带有普通操作符的数据流图(DFG)。元操作分割和组合算法用硬件特性作为输入,将图级别的IR提升为的Sparse IR。然后,我们使用DFG转换通道将Sparse IR再次下降到图级别的IR。在此过程中,原始DFG中的GEMM节点被元操作(“切片”矩阵乘法)替换。我们在此步骤中实现的DFG被命名为MetaDFG。Meta-DFG进一步下降到编译器后端的低级IR,如Halide IR和AKG IR。布局转换操作符消除pass和元操作融合pass被添加到后端,以优化低级IR并最终为每个SpMM生成高效的内核代码。
Sparse IR
稀疏矩阵乘法(SpMM)可以分为两类,输入稀疏SpMM和输出稀疏SpMM。特征上,在卷积神经网络(CNN)中,稀疏性是由权重剪枝技术引起的,从而导致输入稀疏SpMM(SDMM)。至于Transformer中的稀疏注意力模块,稀疏分数矩阵使得($Q \times K^T$)成为输出稀疏SpMM(SDDMM)。
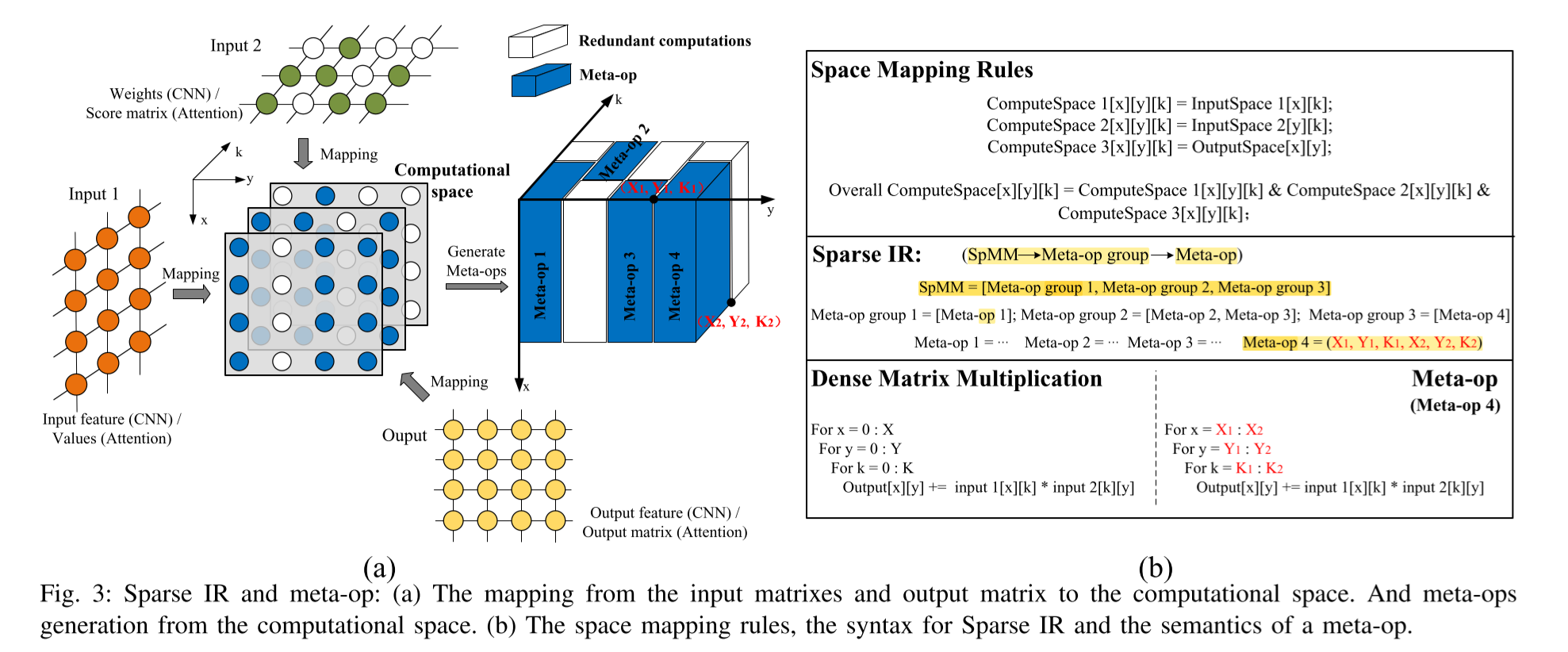
在三维计算空间中沿第三维广播数据空间中的二维矩阵,然后我们将三个矩阵的广播结果取AND,以获得最终的计算空间的稀疏性。
在SpMMPlu中,我们将一个长方体中相邻的非零元素聚集为基本计算单元,称为元操作(meta op)。以图3(a)中的计算空间为例,该空间中生成了四个元操作。通过将元操作的计算过程(例如,图3(b)中的元操作4)与密集的GEMM(广义矩阵乘法)进行比较,我们可以发现元操作本质上是一个“切片”的密集GEMM。它们具有相同的计算范式,唯一的区别在于循环边界。
Sparse IR是一种多层次的IR,根据空间架构中的多层次并行性/顺序性来表示不同粒度的计算。在这里,我们使用subIR来表示Sparse IR中更细粒度的计算。对于典型的GPGPU,Sparse IR采用三层结构组织,即SpMM操作符sub-IR、元操作组sub-IR和元操作sub-IR。每个最内层的元操作sub-IR由计算空间中两个关键点的坐标组成,以唯一标识特定的元操作。两个关键点的坐标直接决定了特定元操作的循环边界。元操作sub-IR与GPGPU中的线程相匹配(例如,NVIDIA V100 GPU中的wmma),元操作组sub-IR代表元操作的并行性,与GPGPU中的线程块相匹配(同一内核中的元操作组中的元操作映射到不同的块)。SpMM操作符sub-IR代表元操作组之间的顺序性,与GPGPU中的内核级序列化相匹配。通过这种方式,元操作组(GPGPU中的cuda/opencl内核)将按顺序执行以完成整个SpMM操作符的计算。
如何生成Sparse IR?首先讨论元操作的生成。设计了一种硬件特性感知的策略,使用硬件抽象作为元操作的初始最小尺寸,这确保了硬件资源最细粒度的高利用率。然而,我们更倾向于使用大的元操作,因为较大的元操作能更好地利用局部性,从而在计算上更加高效。起初,重写掩码中的每个非零元素都是一个1×1×1的元操作,然后我们对每个元操作进行迭代,尽可能将更小的元操作组合成更大的元操作。例如,在第一次迭代中,1×1×1的元操作可能会根据周围元操作的不同聚合程度扩展为2×2×2(图4中的类型1)、2×2×1(图4中的类型2)和2×1×1(图4中的类型3)的更大元操作尺寸。
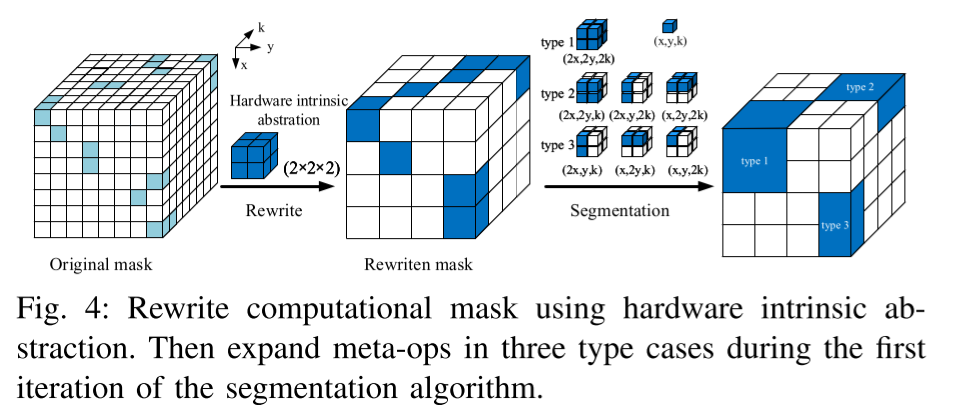
接下来讨论元操作组的生成。由于GPU上的线程以线程块为单位调度,因此将相同大小的元操作组合在一起作为一个元操作组,实现均衡的工作负载。具有加法关系的元操作不应放到同一个组中(即同一组中的元操作不能对应重复的输出元素)以避免极其昂贵的原子加法操作。最后假如一些组中的元操作太少,则将几个没有加法关系的原操作组组合在一起,以提高硬件利用率。
代码生成
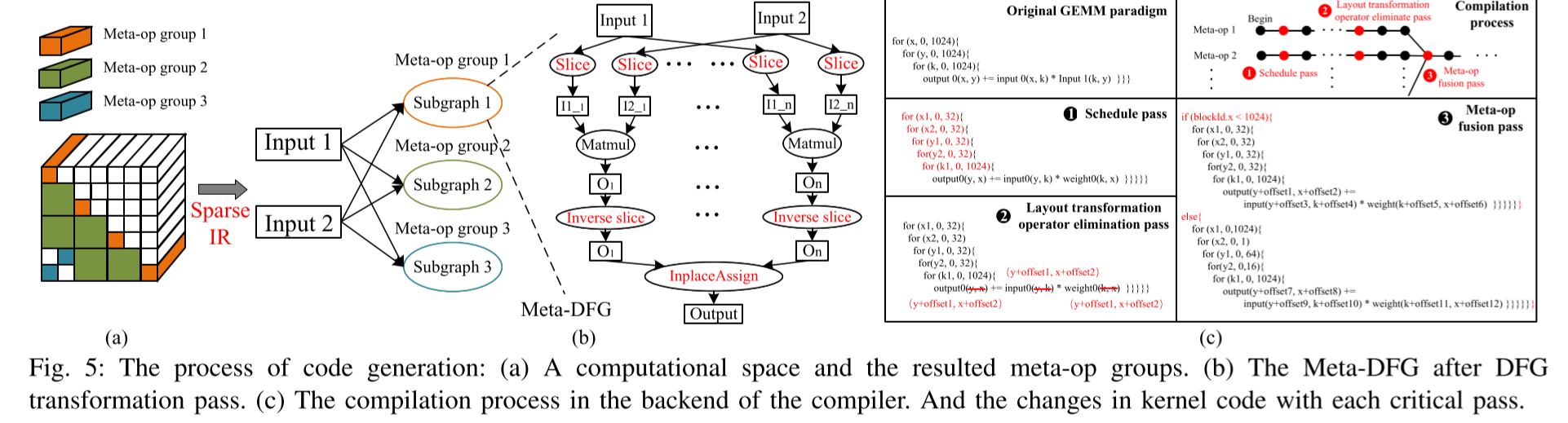
DFG转换pass:DFG转换通道根据相应的Sparse IR将原始DFG转换为Meta-DFG。具体来说,对于图5(a)中的计算空间,DFG转换通道将原始表示密集GEMM的单个图转换为具有三个子图的图,其中每个子图对应于图5(b)中所示的元操作组。在每个子图中,我们在原始DFG的输入侧插入切片节点,以为每个元操作提供特定的输入数据。在每个矩阵乘法节点之后,我们插入逆切片节点以将切片的数据恢复到全局数据格式。最后,我们插入一个原地赋值节点,将每个元操作的所有输出张量聚集在一起,以实现最终的输出张量。
Layout transformation elimination pass:这个pass的实质是,我们发现通常可以通过稍微更改计算密集型算子的内核代码,将布局转换操作合并到其中。具体来说,在CNN和Transformer中的SpMM编译过程中,此通道的效果反映在两个方面。首先,对于范式优化通道后的低级IR,这个pass根据Sparse IR的元操作的位置信息,将IR中的三个张量的索引加上一个偏移量,如图5(c)中的❷,就可以消除数据布局转换。
元操作融合pass:通过在内核代码中添加块条件判断语句(如❸所示),将元操作组中的元操作合并到单个内核中。
实验结果:
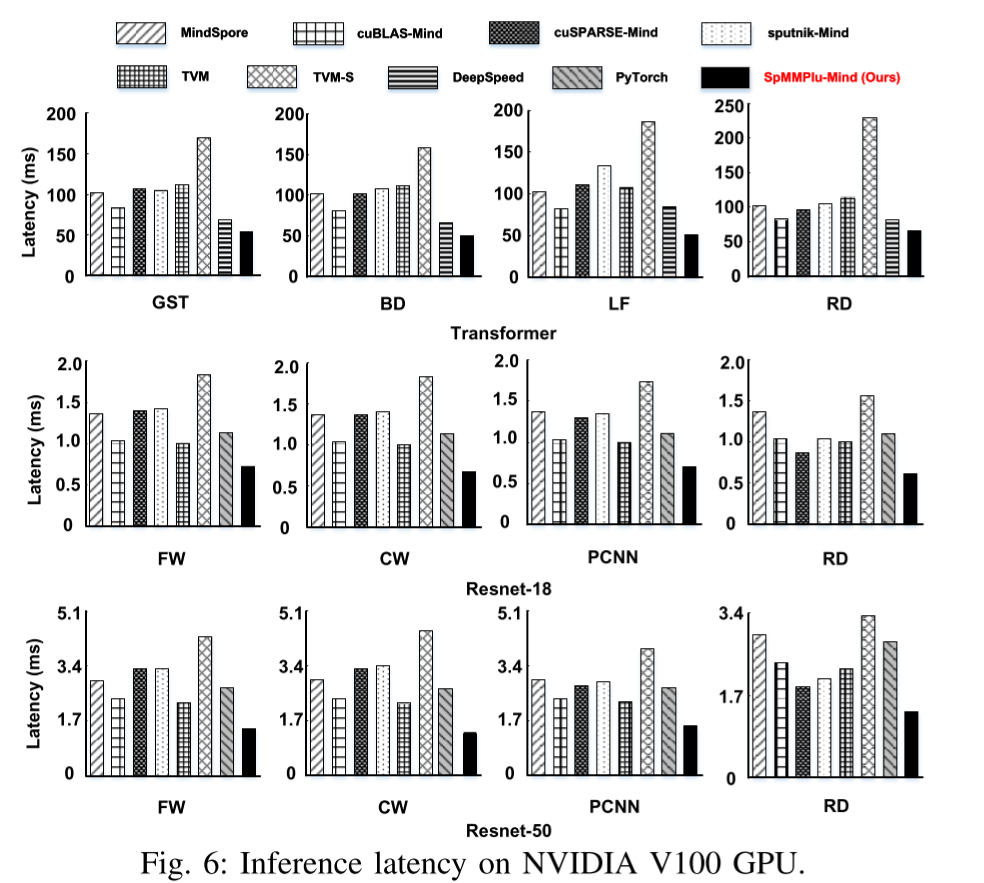
想法:输出稀疏是怎么实现的?是否可以扩展到其他算子?