作者: Junhui He 邮箱：zeonfaiho@yeah.net

GPU编程学习笔记

CS 179: GPU Programming (caltech.edu)

基本概念

简单的例子

GPU的特点：允许我们同时运行数千个线程（实际的情况是这些线程并非真的同时运行，只是它们之间上下文切换的开销很小）。

GPU执行计算的通常流程：

• 在主机（CPU可直接访问的内存）上设置输入
• 在主机上为输出分配内存
• 在GPU上为输入分配内存
• 在GPU上为输出分配内存
• 将输入从主机复制到GPU（慢）
• 启动GPU内核（快）
• 将输出从GPU复制到主机（慢）

注意：复制操作可以是异步的，而且有统一内存管理可用。

未使用统一内存管理：

#include <stdio.h>
#include <cuda_runtime.h>

__global__ void vectorAdd(const float *A, const float *B, float *C, int numElements)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;

    if (i < numElements)
    {
        C[i] = A[i] + B[i];
    }
}

int main()
{
    int numElements = 50000;
    size_t size = numElements * sizeof(float);
    float *h_A = (float *)malloc(size);
    float *h_B = (float *)malloc(size);
    float *h_C = (float *)malloc(size);

    float *d_A, *d_B, *d_C;
    cudaMalloc((void **)&d_A, size);
    cudaMalloc((void **)&d_B, size);
    cudaMalloc((void **)&d_C, size);

    cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);

    vectorAdd<<<10, 5000>>>(d_A, d_B, d_C, numElements);

    cudaMemcpy(h_C, d_C, size, cudaMemcpyDeviceToHost);

    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);

    free(h_A);
    free(h_B);
    free(h_C);

    return 0;
}

使用统一内存管理并自动拷贝：

#include <stdio.h>
#include <cuda_runtime.h>

__global__ void vectorAdd(float *A, float *B, float *C, int numElements)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;

    if (i < numElements)
    {
        C[i] = A[i] + B[i];
    }
}

int main()
{
    int numElements = 50000;
    size_t size = numElements * sizeof(float);
    float *h_A, *h_B, *h_C;

    cudaMallocManaged(&h_A, size);
    cudaMallocManaged(&h_B, size);
    cudaMallocManaged(&h_C, size);

    vectorAdd<<<10, 5000>>>(h_A, h_B, h_C, numElements);

    cudaDeviceSynchronize();

    cudaFree(h_A);
    cudaFree(h_B);
    cudaFree(h_C);

    return 0;
}

手动预取：

#include <stdio.h>
#include <cuda_runtime.h>

__global__ void vectorAdd(float *A, float *B, float *C, int numElements)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;

    if (i < numElements)
    {
        C[i] = A[i] + B[i];
    }
}

int main()
{
    int numElements = 50000;
    size_t size = numElements * sizeof(float);
    float *h_A, *h_B, *h_C;

    cudaMallocManaged(&h_A, size);
    cudaMallocManaged(&h_B, size);
    cudaMallocManaged(&h_C, size);

    // Prefetch data to GPU device
    cudaMemPrefetchAsync(h_A, size, 0);  // 0 is the device ID for the GPU
    cudaMemPrefetchAsync(h_B, size, 0);
    cudaMemPrefetchAsync(h_C, size, 0);

    vectorAdd<<<10, 5000>>>(h_A, h_B, h_C, numElements);

    // Prefetch data back to CPU
    cudaMemPrefetchAsync(h_C, size, cudaCpuDeviceId);

    cudaDeviceSynchronize();

    cudaFree(h_A);
    cudaFree(h_B);
    cudaFree(h_C);

    return 0;
}

异步数据复制：

#include <stdio.h>
#include <cuda_runtime.h>

__global__ void vectorAdd(const float *A, const float *B, float *C, int numElements)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;

    if (i < numElements)
    {
        C[i] = A[i] + B[i];
    }
}

int main()
{
    int numElements = 50000;
    size_t size = numElements * sizeof(float);
    float *h_A = (float *)malloc(size);
    float *h_B = (float *)malloc(size);
    float *h_C = (float *)malloc(size);

    // Initialize host memory
    for (int i = 0; i < numElements; ++i) {
        h_A[i] = i;
        h_B[i] = i;
    }

    float *d_A, *d_B, *d_C;
    cudaMalloc((void **)&d_A, size);
    cudaMalloc((void **)&d_B, size);
    cudaMalloc((void **)&d_C, size);

    // Create a stream
    cudaStream_t stream;
    cudaStreamCreate(&stream);

    // Asynchronously copy data to GPU
    cudaMemcpyAsync(d_A, h_A, size, cudaMemcpyHostToDevice, stream);
    cudaMemcpyAsync(d_B, h_B, size, cudaMemcpyHostToDevice, stream);

    // Launch kernel in the same stream
    vectorAdd<<<10, 5000, 0, stream>>>(d_A, d_B, d_C, numElements);

    // Asynchronously copy data back to host
    cudaMemcpyAsync(h_C, d_C, size, cudaMemcpyDeviceToHost, stream);

    // Wait for the stream to finish
    cudaStreamSynchronize(stream);

    // Clean up
    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);
    cudaStreamDestroy(stream);

    free(h_A);
    free(h_B);
    free(h_C);

    return 0;
}

基本概念

一些基本的概念：

• CUDA：Nvidia的类C++编程语言，用于编程图形处理单元（GPU）。
• nvcc：nVidia CUDA编译器。
• SM：流多处理器（Streaming Multiprocessor）。
• SIMT计算：单指令，多线程（Single Instruction, Multiple Threads）
• 线程（Threads） - 一个执行线程是被编程的指令中的最小序列，可以由一个调度器（scheduler）独立管理，这通常是操作系统的一部分。
• 线程块（Blocks） - 线程块是一个编程抽象，代表一组可以串行或并行执行的线程。
• 网格（Grids） - 编程抽象，代表所有线程块。
• Warp（线束） - 在硬件上，一个线程块是由“warps”组成的。一个warp是一个线程块中的32个线程，线程块以warp为单位执行；一个warp中所有线程都执行相同的指令。这些线程被SM串行地选择。
• Warp分歧（Warp Divergence） - 所有线程通常必须执行相同的代码（if-then-else）；假如某些线程需要执行不同的分支，则这些分支将会顺序执行。
• 每个线程块都在一个SM上完整地执行，但是一个SM可以同时执行多个线程块，具体数量取决于资源（如寄存器、共享内存等）的可用性。

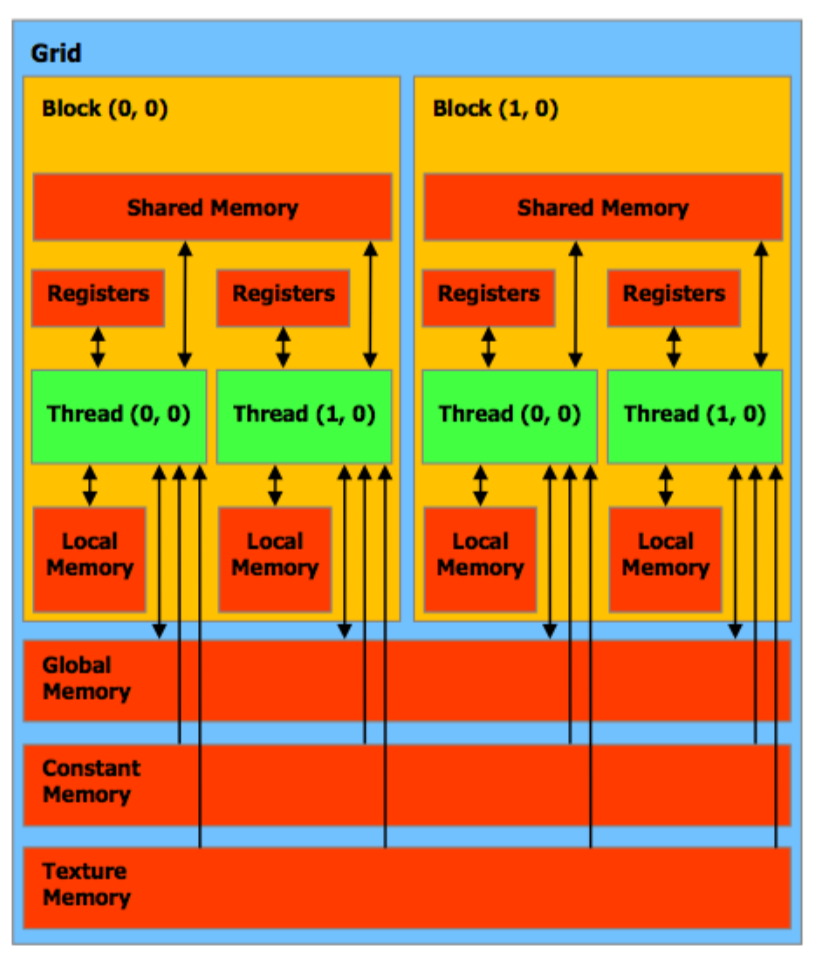
对于许多涉及数组的可并行化问题，考虑多维数组是必要的。我们希望为多维对象分配唯一的线程索引。因此，CUDA提供了内置的多维（最高3维）线程索引功能，这是通过一个名为dim3的结构体实现的。

一些题外话：SIMD vs. SIMT

SIMD：

• SIMD描述了一类指令，这些指令可以同时对多个寄存器执行相同的操作。
• 示例：将某标量加到3个寄存器上，将每次加法的输出存储在这些寄存器中。
• 用于增加像素的亮度。
• CPU也有SIMD指令，对于需要进行大量数值计算的应用非常重要。

• 视频编解码器，如x264/x265，大量使用SIMD指令来加速视频的编码和解码。

• 将算法转换为使用SIMD通常被称为“向量化”。
• 并不是所有的算法都能从中受益或者完全被向量化。
• 使用SIMD指令并不总是有益的。
  • 即使使用SIMD硬件也需要额外的功率，从而产生浪费的热量。
  • 如果收益很小，那么可能不值得增加额外的复杂性。
• 优化编译器如GCC和LLVM仍在被训练，以能够有用地向量化代码，尽管在过去的2年里这一领域已经有了许多令人兴奋的发展，并且是一个活跃的研究领域。
• Polly LLVM 官网

SIMT：

领域：计算机科学与并行计算

翻译：

• CUDA的计算模型使用的是SIMD的一个较为宽松的扩展。
  • 关键区别：
    • 单指令，多寄存器集。
      • 浪费了一些寄存器，但主要是为了满足以下两点。
    • 单指令，多地址（即并行内存访问）
      • 内存访问冲突！我们将在下周讨论。
    • 单指令，多流程路径（即允许使用if语句）
      • 引入了速度降低，称为“线程束分歧”。

值得一提的是GPU的一些硬件限制：

• 每个块的最大线程数通常是512或1024，具体取决于机器。
• 每个网格的最大线程块数通常是65535。
  • 如果你超过了这些数字，你的GPU可能会报错或输出垃圾数据。
• GPU编程的很大一部分是处理这种硬件限制。
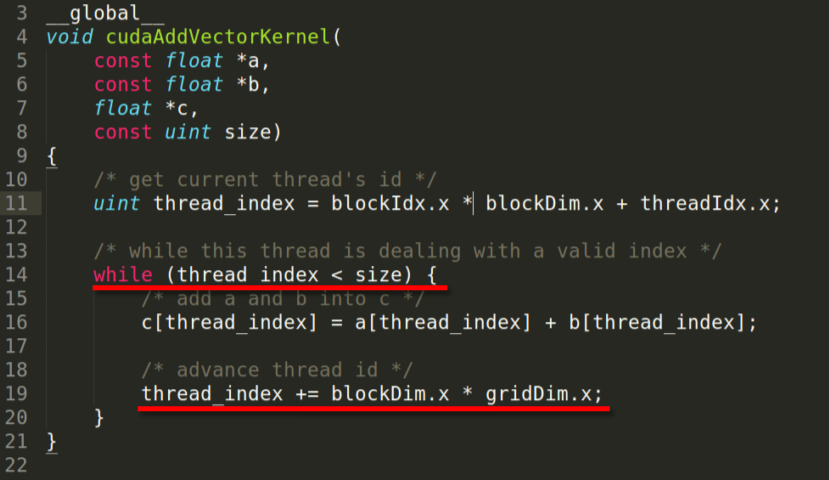
• 这种限制也意味着kernel必须补偿可能没有足够的线程单独分配给数据的事实。

CUDA程序优化

访存优化

GPU内存层级中，特殊之处在于存在共享内存（shared memory）

共享内存：被创建它的块中的任何线程访问。它的生命周期与块相同。当没有bank冲突或从不同线程从相同地址写入数据时，它的速度可以与寄存器一样快。

全局内存：全局内存IO是GPU上最慢的IO形式（更慢的可能是访问主机内存）。正因为如此，我们希望尽可能少地访问全局内存。一种与GPU硬件相容性好的访问模式被称为合并内存访问。

• 一组内存访问通过一次内存事务来完成
• 合并内存访问最小化了通过这些内存事务读入的缓存行数量
  • GPU的缓存行是128字节并且是对齐的
  • 因此假如对全局内存的访问是128字节对齐的话，效率会高得多

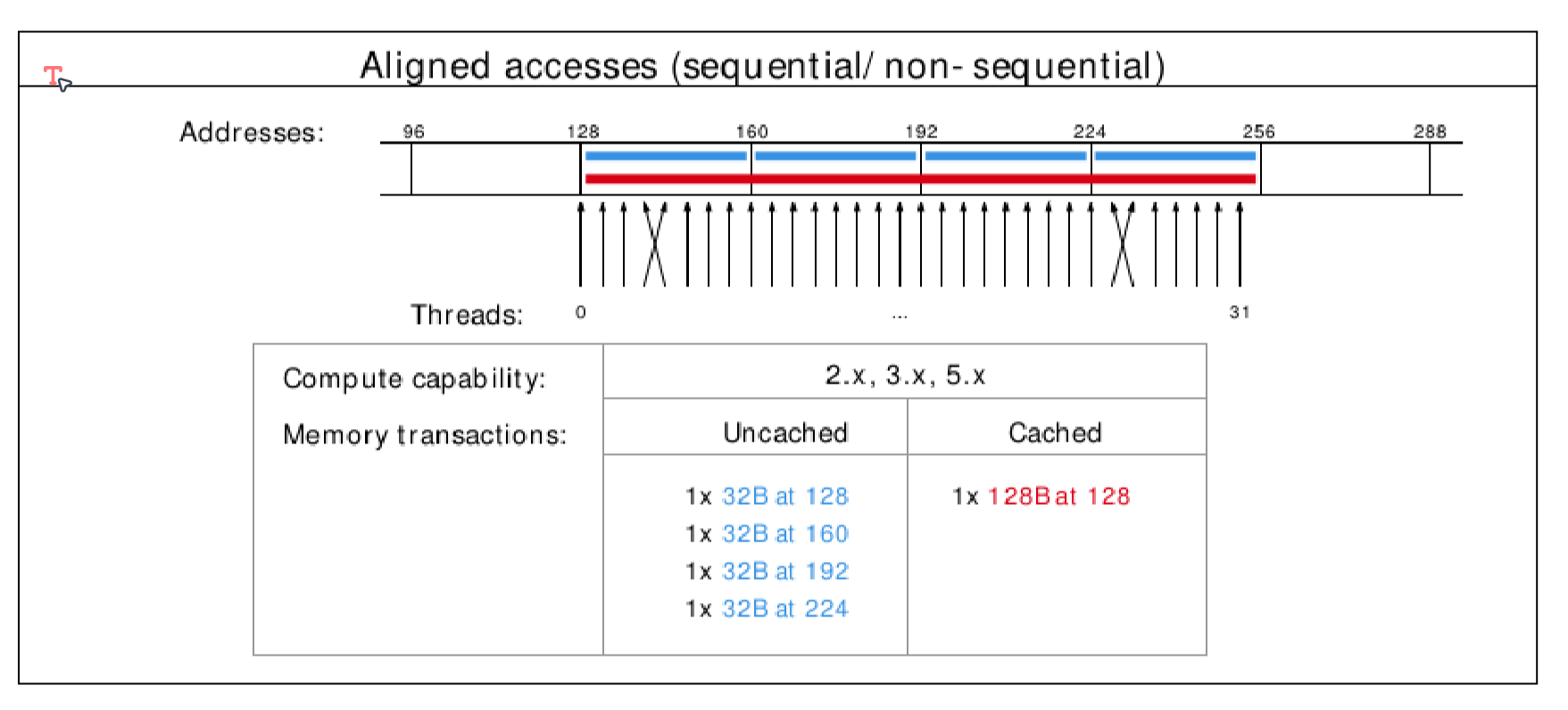
共享内存：

• 位于SM中的非常快速的内存
• 与L1缓存相同的硬件
• 延迟大约为~5ns
• 最大大小约为~48KB（根据GPU而异）
• 共享内存的可见范围是线程块
• 可以静态地分配共享内存（编译时已知大小）或动态地分配（直到运行时才知道大小）。
• 静态分配语法：
  • __shared__ float data[1024];
  • 在内核中声明，主机代码中无任何内容。
• 动态分配语法：
  • 主机：
    • kernel<<<grid_dim, block_dim, numBytesShMem>>>(args);
  • 设备（在内核中）：
    • extern __shared__ float s[];

一个使用共享内存的例子：

• 任务：计算字节频率计数
• 输入：长度为n的字节数组
• 输出：包含每个字节出现次数的256个元素的整数数组

朴素方法：在全局内存中更新结果，n次全局存储

聪明方法：在共享内存中更新结果，最后复制到全局内存；每个线程块256次全局存储。

流程：

• 从全局内存复制到共享内存
• syncthreads()
• 执行计算，逐步在共享内存中输出，并在必要时调用__syncthreads()
• 将输出从共享内存复制到全局内存中的输出数组

共享内存被设置为32个bank

• 如果你将共享内存划分为4字节长的元素，那么元素i位于bank i % 32中。

• 当一个warp中的2个线程访问同一bank的不同元素时，会发生bank冲突。

• bank冲突导致串行内存访问而不是并行。

解决方法：

• 跨度1 ⇒ 32个线程分别访问bank 0, 1, 2, …, 31，没有冲突
• 跨度2 ⇒ 32个线程分别访问bank 0, 2, 4, .. , 30, 0, 2, 4, …；2路bank冲突
• 跨度3 ⇒ 无冲突
• 跨度4 ⇒ 4路bank冲突
• …
• 跨度32 ⇒ 32路bank冲突

（n路冲突，n=gcd(stride, 32)）

为了解决跨度32的情况，我们将浪费一个字节进行填充，使跨度变为33。

同步与并行

前面提到了线程同步；通常使用__syncthreads()函数来同步一个块内的线程

• 仅在块级别起作用
• SMs (流多处理器) 是相互独立的，不能实现线程块之间的同步
• 与C/C++中的barrier()函数相似
• 对于使用共享内存的内核，__synchthreads()调用非常有用。

此外还有原子操作，用来避免多个线程同时对某个数据进行操作：

CUDA 提供了内置的原子操作。

• 使用函数：atomic<op>(float *address, float val);
• 将 <op> 替换为：Add、Sub、Exch、Min、Max、Inc、Dec、And、Or、Xor 中的一个。
• 例如，使用 atomicAdd(float *address, float val) 进行原子加法操作。

如果你想通过将数字加到一个初始值为0的变量来累加N个数，你必须一次加一个数；但不要这么做，更优的做法是：

• 使用共享内存在一个块内求和

• 每个线程块求和后，在全局内存中执行一次的atomicAdd操作。

指令级（ILP）并行性是当你避免因指令依赖性而引起的性能损失时的情况。

方法：循环展开

GPU占用率

为什么占用率很重要？因为每个流多处理器（SM）需要足够的独立线程来隐藏延迟

• 指令延迟

• 内存访问延迟

• 占用率 = 每个SM上的活动warp数 / 每个SM的最大warp数

决定每个SM能够容纳的线程数（即每个SM的最大warp数）是由GPU的硬件资源所决定的。线程/块很重要，因为它（结合块的数量）告诉我们SM上有多少warp。

什么情况下，更高的占用率可以提高性能？

• 每个线程有更多的独立工作（无需与其他线程交互、无需读写内存） -> 需要的占用率较低
• 访存密集的代码往往需要更高的占用率——需要更多的工作来隐藏它。

本章总结

• 并行优化
  • 隐藏延迟：提高占用率
  • 指令级并行（ILP）：循环展开
  • warp内的线程执行一致性
• 访存优化
  • 全局内存：
    • 读：合并访存；
    • 写：在共享内存中提前规约；
  • 共享内存：避免bank冲突

一些值得注意的点

cuda是如何将block里面的线程分为warp的？

线程在它们所属的线程块内有一个唯一的线程ID。通常情况下，一个线程块中的前32个线程（线程ID 0到31）会被组织成一个warp，接下来的32个线程（线程ID 32到63）会被组织成下一个warp，依此类推。

那线程id是如何计算的？ \(\text{ThreadID}_{\text{block}} = \text{threadIdx}.x + \text{threadIdx}.y \cdot \text{blockDim}.x + \text{threadIdx}.z \cdot \text{blockDim}.x \cdot \text{blockDim}.y\) 所以实际上，z表示表号，y表示行号，x表示列号，和直觉上的判断正好相反

知道如何划分warp是相当有用的，可以帮助我们识别访存模式（合并访存、避免bank冲突etc.）

高性能Transpose算子

• shared memory：-60%
• avoid bank conflict: -10%
• ILP: -10%

__global__
void shmemTransposeKernel(const float *input, float *output, int n) {
    // TODO: Modify transpose kernel to use shared memory. All global memory
    // reads and writes should be coalesced. Minimize the number of shared
    // memory bank conflicts (0 bank conflicts should be possible using
    // padding). Again, comment on all sub-optimal accesses.

    // input [j : j + 4, i] -> [block_j * 4 : block_j * 4 + 3, block_i]
    // output [i, j : j + 4] -> [block_i, block_j * 4 : block_j * 4 + 3]

    __shared__ float shared_input[64 * 64];
    __shared__ float shared_output[65 * 64];

    // int i = threadIdx.x + 64 * blockIdx.x;
    // int j = 4 * threadIdx.y + 64 * blockIdx.y;

    int block_i0 = 64 * blockIdx.x;
    int block_j0 = 64 * blockIdx.y;

    int block_i = threadIdx.x;
    int block_j = threadIdx.y * 4;

    for (; block_j < threadIdx.y * 4 + 4; block_j++) {
        shared_input[block_i + 64 * block_j] = input[block_i0 + block_i + n * (block_j0 + block_j)];
        shared_output[block_j + 65 * block_i] = shared_input[block_i + 64 * block_j];
    }

    __syncthreads();

    block_i0 = 64 * blockIdx.y;
    block_j0 = 64 * blockIdx.x;

    block_i = threadIdx.x;
    block_j = threadIdx.y;

    for (; block_j < threadIdx.y * 4 + 4; block_j++) {
        output[block_i0 + block_i + n * (block_j0 + block_j)] = shared_output[block_i + 65 * block_j];
    }
}

加入循环展开（收益不大）

__global__
void optimalTransposeKernel(const float *input, float *output, int n) {
    // TODO: This should be based off of your shmemTransposeKernel.
    // Use any optimization tricks discussed so far to improve performance.
    // Consider ILP and loop unrolling.

    __shared__ float shared_output[64 * 64];

    // int i = threadIdx.x + 64 * blockIdx.x;
    // int j = 4 * threadIdx.y + 64 * blockIdx.y;

    int block_i0 = 64 * blockIdx.x;
    int block_j0 = 64 * blockIdx.y;

    int block_i = threadIdx.x;
    int block_j = threadIdx.y * 4;

    float s0 = input[block_i0 + block_i + n * (block_j0 + block_j)];
    float s1 = input[block_i0 + block_i + n * (block_j0 + block_j + 1)];
    float s2 = input[block_i0 + block_i + n * (block_j0 + block_j + 2)];
    float s3 = input[block_i0 + block_i + n * (block_j0 + block_j + 3)];

    shared_output[block_j + 64 * block_i] = s0;
    shared_output[block_j + 1 + 64 * block_i] = s1;
    shared_output[block_j + 2 + 64 * block_i] = s2;
    shared_output[block_j + 3 + 64 * block_i] = s3;

    __syncthreads();

    block_i0 = 64 * blockIdx.y;
    block_j0 = 64 * blockIdx.x;

    block_i = threadIdx.x;
    block_j = threadIdx.y * 4;

    float t0 = shared_output[block_i + 64 * (block_j)];
    float t1 = shared_output[block_i + 64 * (block_j + 1)];
    float t2 = shared_output[block_i + 64 * (block_j + 2)];
    float t3 = shared_output[block_i + 64 * (block_j + 3)];

    output[block_i0 + block_i + n * (block_j0 + block_j)] = t0;
    output[block_i0 + block_i + n * (block_j0 + block_j + 1)] = t1;
    output[block_i0 + block_i + n * (block_j0 + block_j + 2)] = t2;
    output[block_i0 + block_i + n * (block_j0 + block_j + 3)] = t3;

}

GPU编程常用算法

规约

如果操作符满足以下条件，则它是一个规约操作符：

• 它可以将一个数组减少到一个标量值。 (例如，对数组的所有元素求和)。

• 最终结果应该可以从创建的部分任务的结果中获得。

• 满足这些要求的运算符包含整数加法、乘法以及一些逻辑运算符（与、或等）。

GPU专用算法大多面向规约问题。

数组求和问题

float sum = 0.0; 
for (int i = 0; i < N; i++)
	sum += A[i];

Naive implementation:

__global__ void cudaSum_atomic_kernel(const float* const inputs, 
                                      unsigned int numberOfInputs, 
                                      float* output) {

    // 获取线程ID
    unsigned int inputIndex = threadIdx.x + blockIdx.x * blockDim.x;

    float partial_sum = 0.0;

    // 每个线程处理一个特定的元素，由于使用了原子操作，所以不需要担心线程冲突
    if(inputIndex < numberOfInputs) {
        partial_sum = inputs[inputIndex];
        atomicAdd(output, partial_sum);
    }
}

想法：在共享内存中为每个线程存储部分和

• 我们可以在共享内存中累积每个块的部分和，然后用原子操作向全局累加器添加一阵个块的部分和。

但是使用1个线程来计算整个块的部分和似乎不太高效；所以：

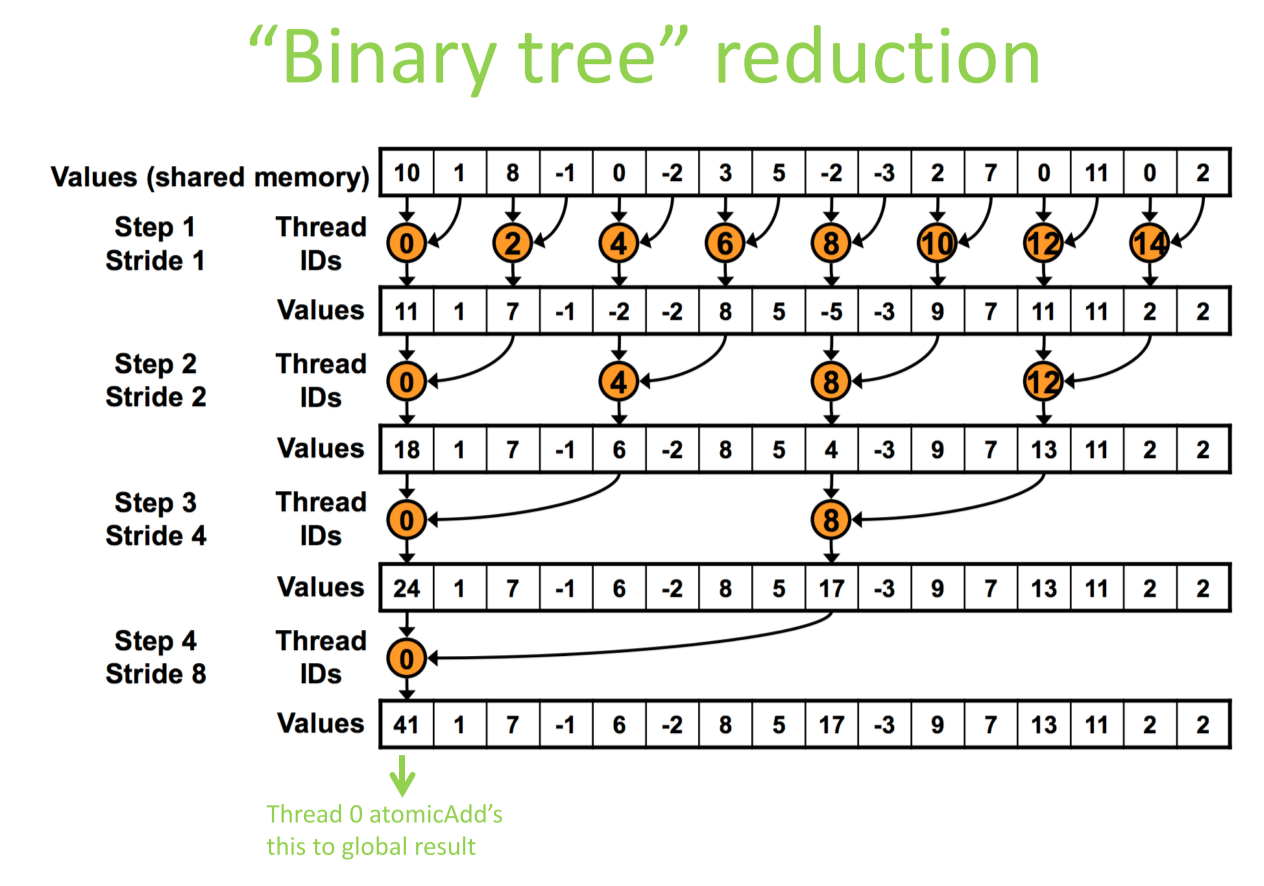
问题：线程发散；step 1只有一半的线程在执行，之后每次减少一半，到最后只有1个线程执行；大量线程空转

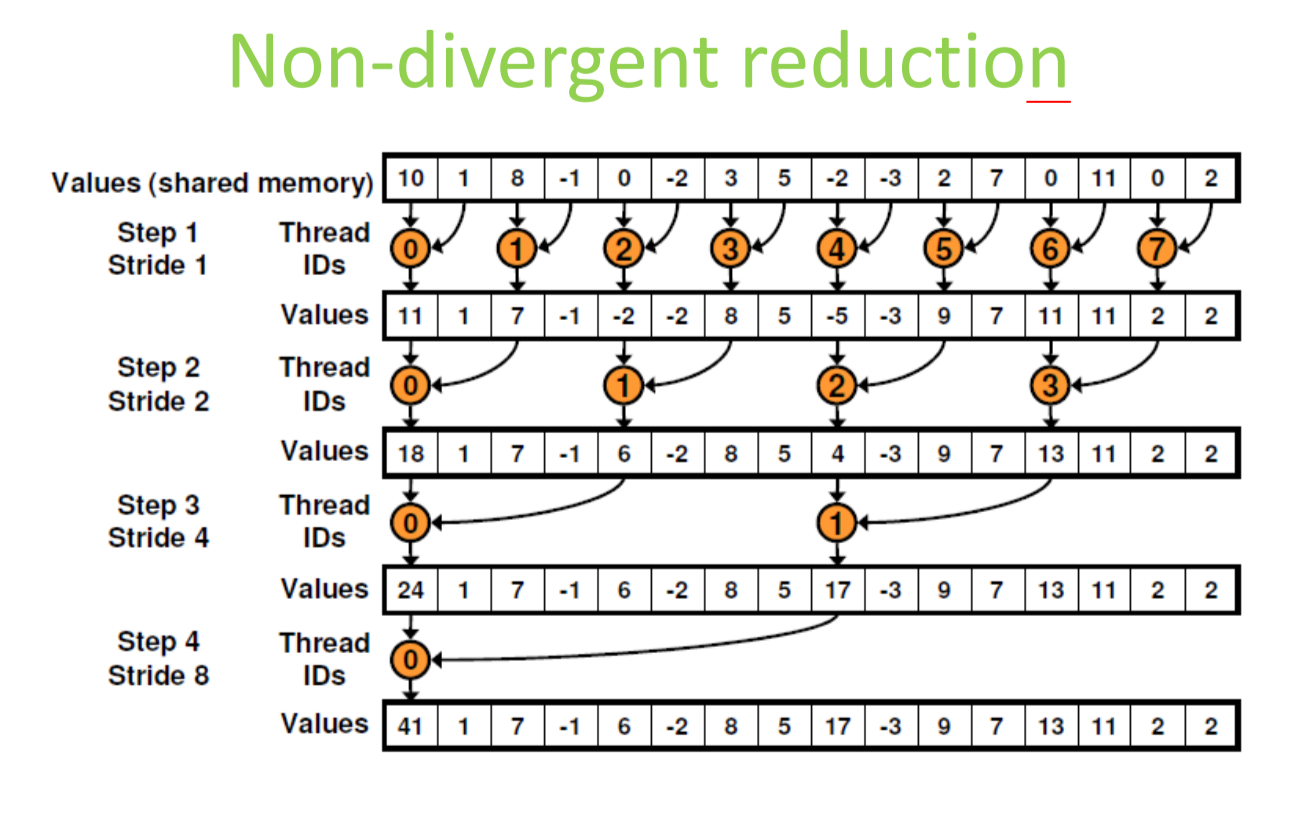
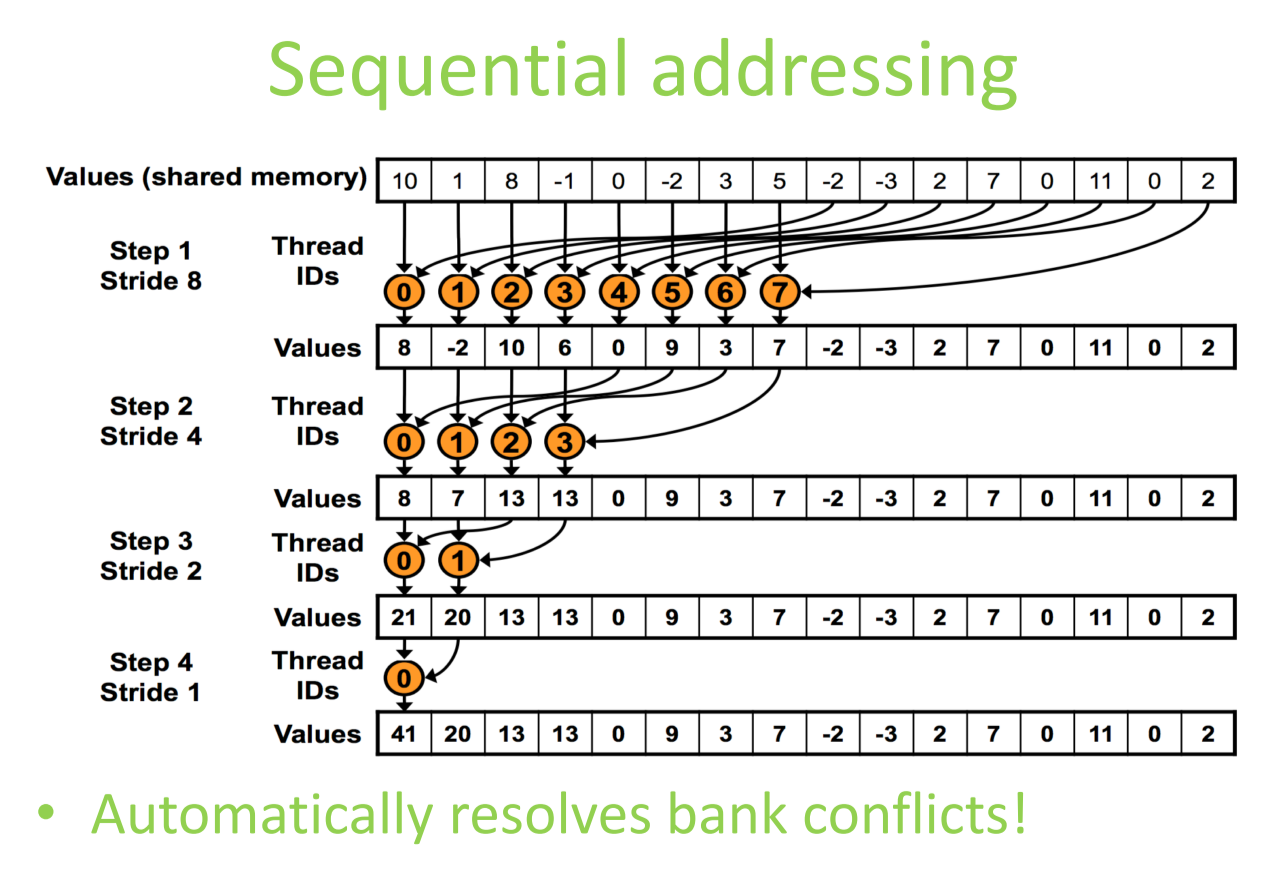
由于stride变成了1，还自动解决了bank冲突问题

最终代码：

__global__ void cudaSum_linear_kernel(const float* const inputs, 
                                      unsigned int numberOfInputs, 
                                      float* output) {
    // 获取线程和块的ID
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;

    // 声明共享内存
    extern __shared__ float partial_outputs[];

    // 计算部分和
    float partial_sum = 0;
    if(idx < numberOfInputs) {
        partial_sum = inputs[idx];
    }
    partial_outputs[tid] = partial_sum;
    
    // 同步确保所有线程都完成了数据加载到共享内存
    __syncthreads();

    // 进行归约操作，进行两两加法
    for(int stride = blockDim.x / 2; stride > 0; stride >>= 1) {
        if(tid < stride) {
            partial_outputs[tid] += partial_outputs[tid + stride];
        }
        __syncthreads(); // 确保在继续下一次迭代之前所有的加法操作已完成
    }

    // 将每个块的结果写回到全局内存
    if(tid == 0) {
        atomicAdd(output, partial_outputs[0]);
    }
}