TFHE:环面上全同态加密方案
主要参考论文:
Chillotti I, Gama N, Georgieva M, et al. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds[C]//international conference on the theory and application of cryptology and information security. Springer, Berlin, Heidelberg, 2016: 3-33. Chillotti I, Gama N, Georgieva M, et al. Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 377-408.
全同态与TFHE
全同态算法在2013年左右大致分为两个大类,一类为 BGV方案,另一类为 GSW方案,而TFHE属于类GSW分支,并且是FHEW方案的一个改进,TFHE方案是目前最快的全同态加密方案。
全同态加密中的噪声
众所周知,全同态加密是有噪声(error)的。假设有一布尔电路如下图:
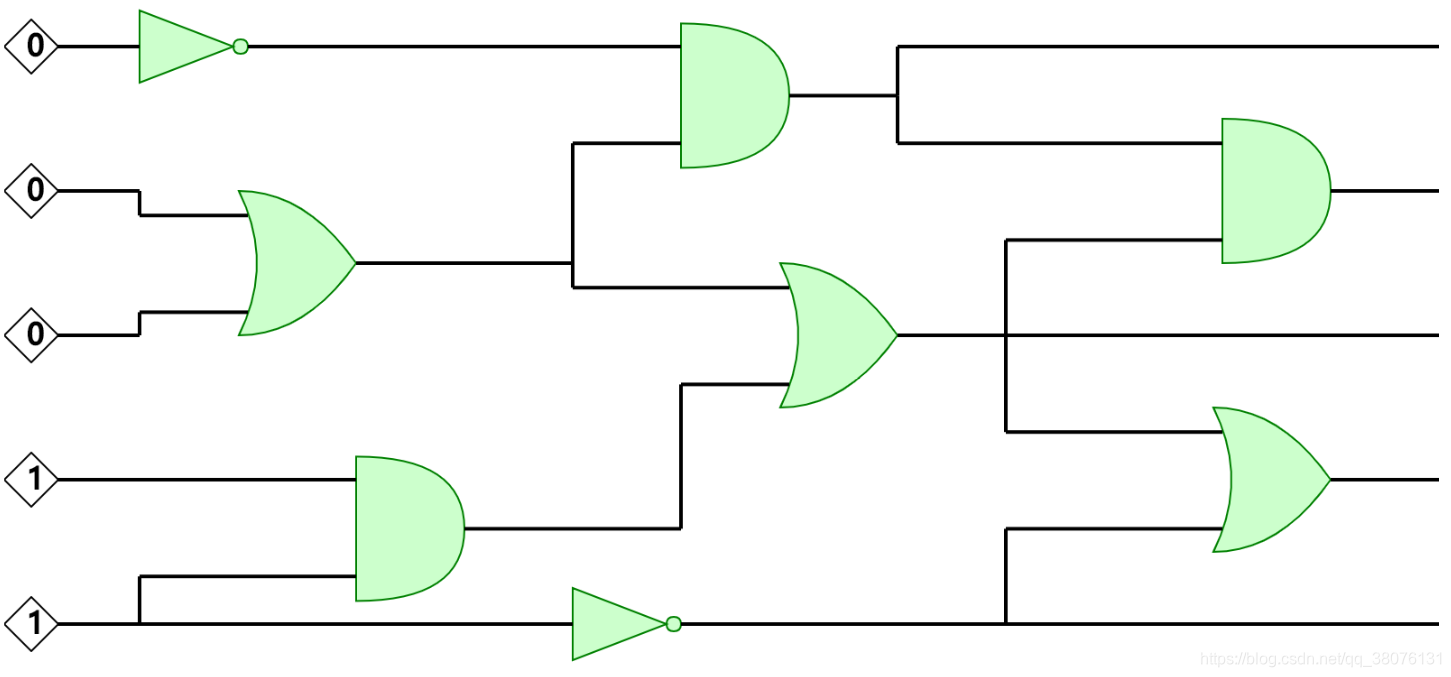
在明文状态下评估该布尔电路,没有任何问题:
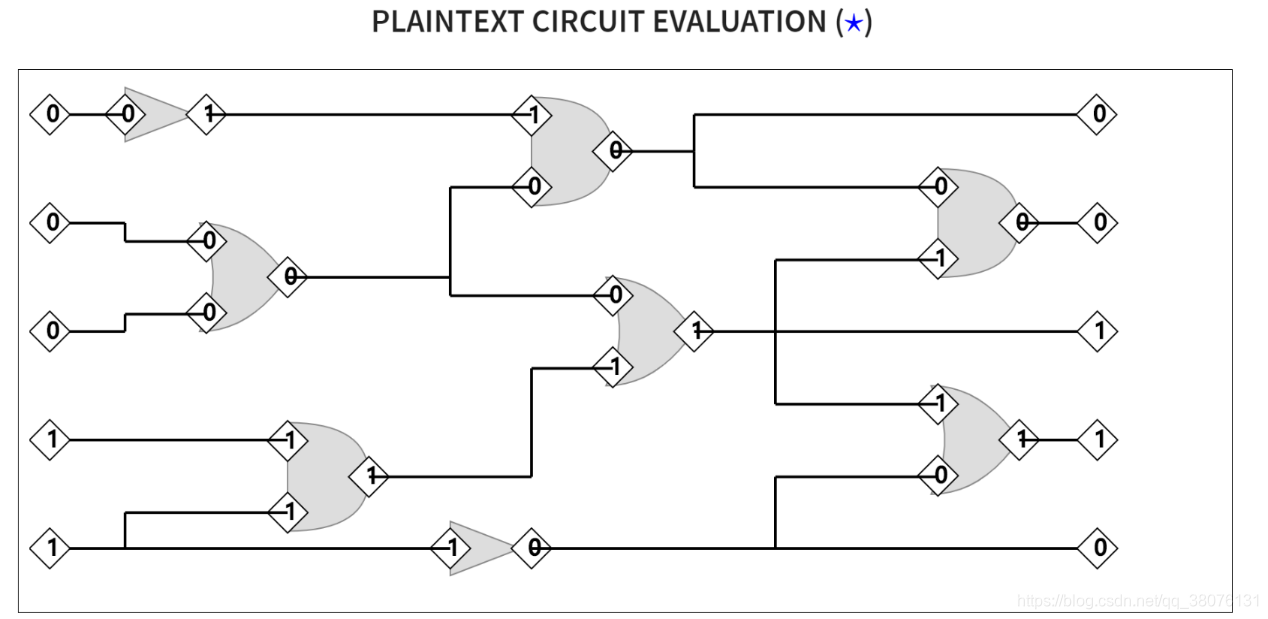
然而,要在全同态加密的密文状态下评估该布尔电路,不但评估时间变得十分漫长,噪声也随着经过的门电路的数量增加而增长,如果经过过多的门电路,则很可能导致最终的解密错误(解密后无法分辨0和1)。 
想要解决同态加密中的噪声问题,目前有如下两种途径:
-
LHE 层级全同态 通过设置LHE中的安全参数,使之足够大从而支持一定深度(depth)的布尔电路的评估。 想象上图中最左端的密文全都有3个level,密文每通过一个 与/或门 就会消耗一个level(取非操作相比于 与/或门 产生可忽略的噪声),如果最终的level小于0则密文不能够正确解密,如下图所示:
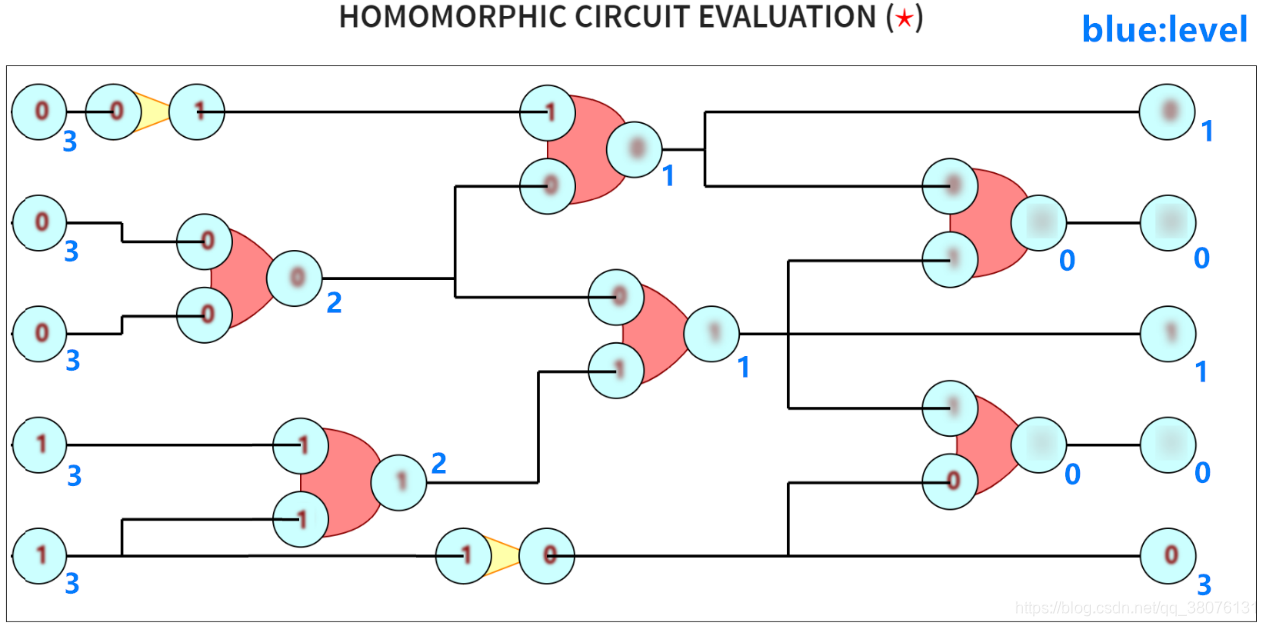
-
Bootstrapping 自举 2009年Gentry提出了自举的设想。整个自举过程如下:
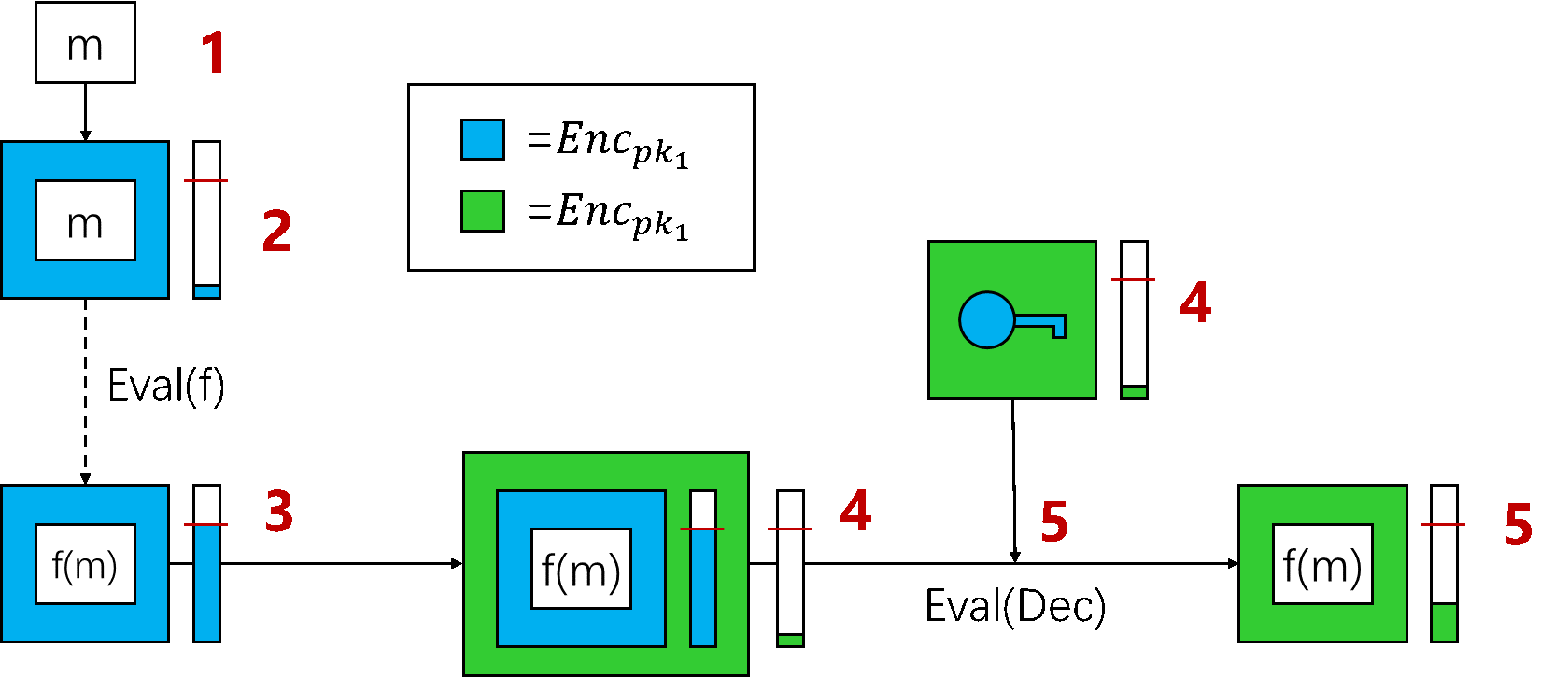

LHE 和 Bootstrapping 两种方案各有优缺点:

TFHE在 LHE 方案和 Bootstrapping 方案中都实现了一定的改进
TFHE
Torus 环面
TFHE全称为:Fully Homomorphic Encryption over the Torus。FHE代表全同态加密,而T代表环面(Torus)。因此,想了解TFHE,在了解什么是FHE后,还要了解什么是环面。 环面大概长下面这张图的样子,像一个甜甜圈(by Ilaria Chillotti): 
实数环面有三条性质:
1.它是一个阿贝尔群(环面上的加法是有定义的)。 2.它拥有 Z-module 结构。 3.它不是一个环(环面上的元素之间的乘法没有定义)。
TFHE 是 FHEW 的改进,主要的优化思路是:使用 LWE 与 GSW 的”外积”,取代 GSW 与 GSW 的“内积”,从而使得计算复杂度降低了一个多项式因子。
TLWE密文的对称加密



TFHE的三种密文形式
除TLWE密文外,TFHE方案中还有两种密文:TRLWE密文与TGSW密文。将TLWE拓展到多项式环面,可得TRLWE密文,将GSW方案拓展至环面,可得TGSW密文。接下来给出TFHE三种密文格式的定义:


下面给出三种密文的明文、密文和密钥的形式,以及可以进行的运算:

TFHE的外积加速
我们发现TLWE密文和TRLWE密文只能进行线性组合,不能进行Product(积)的操作,即只能做加法不能做乘法。TFHE的研究者在定义了TLWE密文和TRLWE密文后,觉得好像离全同态加密还差一点,于是他们从GSW方案中找到了灵感。GSW方案中有一个ring product(内积)的操作: 
输入是两个TGSW samples,Z[X]是整数多项式,输出是一个TGSW sample,解密后得到两个消息的乘积,这里观察到,尽管运算是对称的,但是它产生的噪声是不对称的。TFHE的研究者基于这个特性研究出了TFHE:把其中一个输入换成TLWE类型,然后输出也变成了TLWE类型,计算变成了点乘(外积)。 
噪声本来就不对称,现在更不对称了(更小了)。然后便可以用分解的方法,把原来TGSW的每行拆开,在并行计算,将原来的叉乘(内积)都变成了点乘(外积),得到一个很大的提速。

下面给出内积和外积的具体表达式以及直观的感受:

层次TFHE(TFHE IN LEVELED MODE)
这一部分使用层次TFHE实现一个确定型自动机的评估。使用上面所说的同态外积构造门:

设TGSW密文的消息空间为 { 0 , 1 } ∈ Z [ X ],TLWE密文的消息空间为{ 0 , 1 / 2 } ∈ T [ X ] ,这样噪声中的∣ ∣ μ A ∣ ∣ 1 就没有了(为1)。 接下来为TFHE选择门电路,这里给出四种图灵完备的门电路组合:
1.Or, And, Not DNF logic 2.Xor, And, 1 Multivariate polynomials 3.Nand minimal indeed 4.Mux, 0, 1 Because we get binary decision diagrams for free 在LHE里面通常选择Xor这一组,FHEW选择了与非门,而(level)TFHE选择的是Mux电路,因为它可以几乎没有消耗的做二进制选择(噪声呈线性增长)。 Mux门电路的选择逻辑很简单,如果c为0则输出b,如果c为1则输出a: C M u x ( c , a , b ) = b + c ⊡ ( a − b ) CMux(c,a,b)=b+c⊡(a−b) 
在(level)TFHE的Mux门电路中有不同的线:图中深红色的线成为控制线(Control line),传输TGSW密文,蓝色的先称为数据线(data line),传输TLWE密文。 随后,我们便可以使用Mux门电路构造和评估任意的 查找表/布尔函数(噪声随电路深度的增加线性增长): 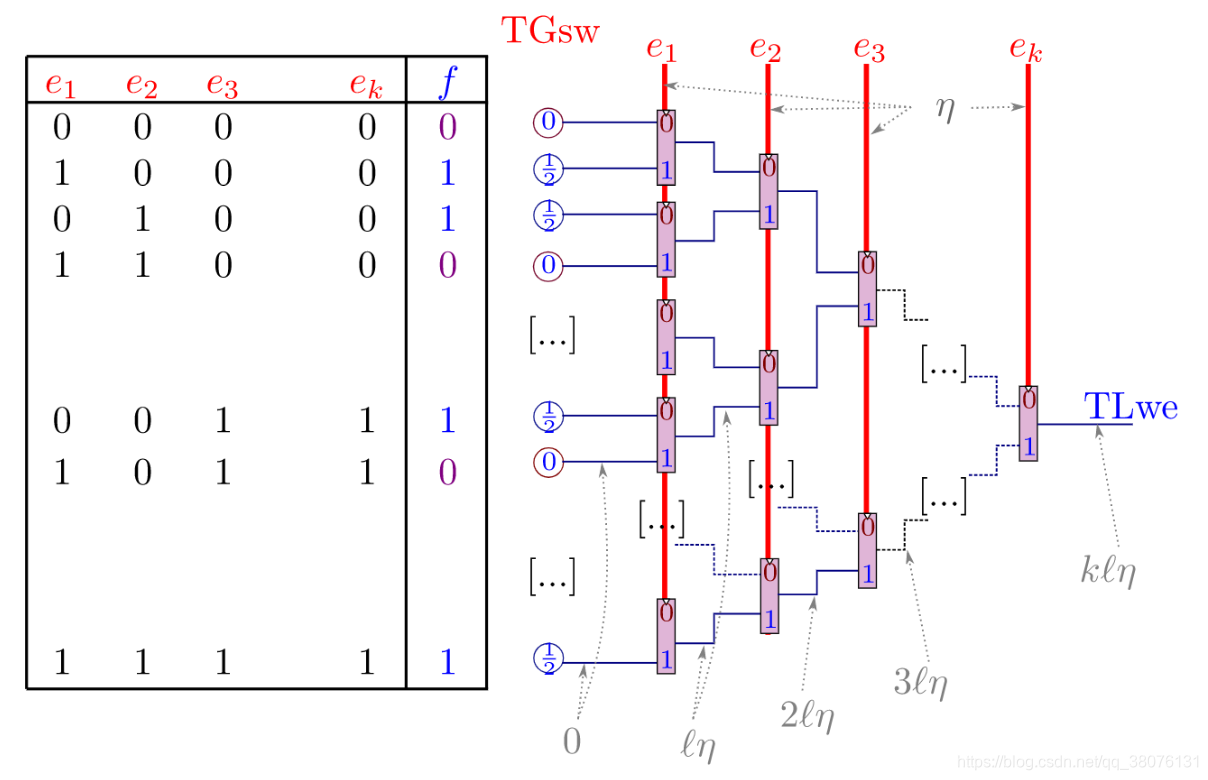
进而可以评估(输入长度已知并固定的)任意确定型(有穷)自动机:
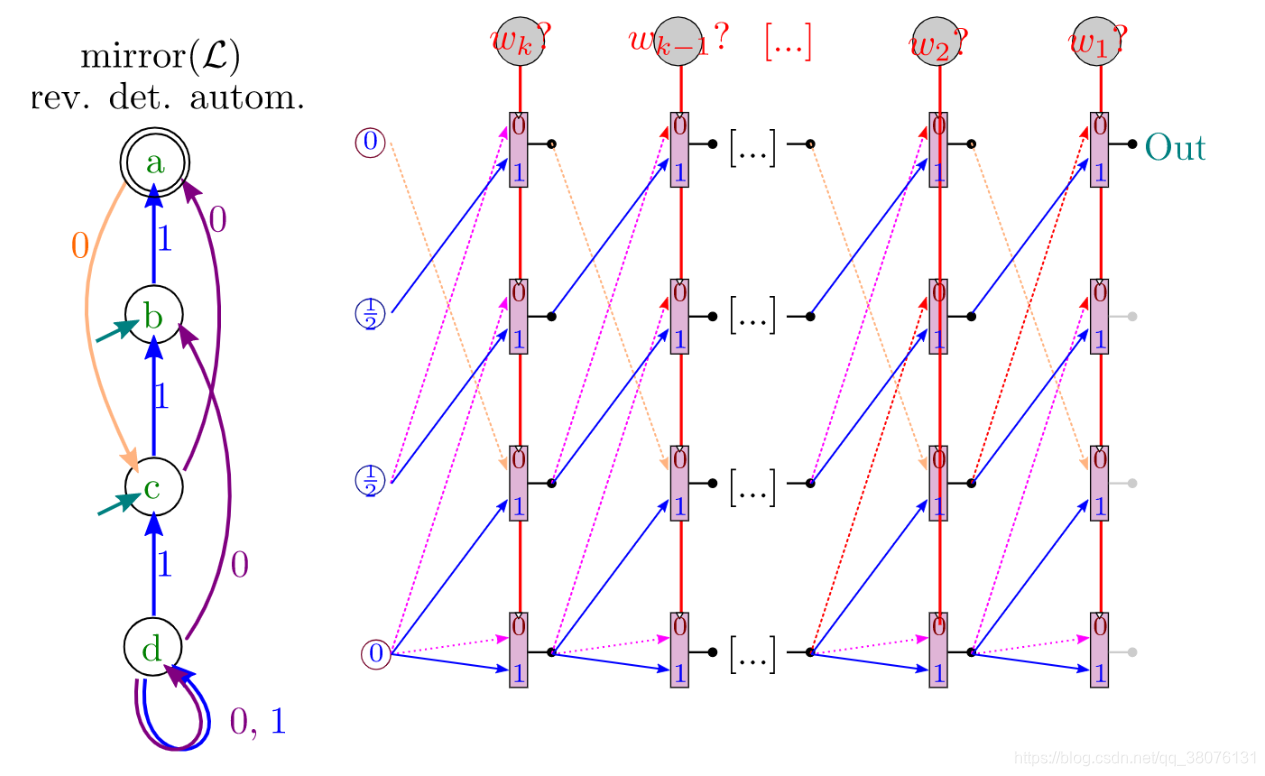
全同态TFHE(TFHE IN FHE MODE)
为实现任意深度电路的同态评估,需要为TFHE引入自举(bootstrapping)操作。 自Gentry于2009年提出自举以来,自举从同态解密(Gentry09),到重加密,到压缩解密函数,再到密钥交换&模交换(FHEW&TFHE使用)。在Gentry09的自举(前面有写)中,自举是一个单独的函数,仅用于减小噪声;而在TFHE中,自举可以改变消息内容。接下来介绍TFHE中的自举门(gate bootstrapping)。
我们现在有一个二进制的消息空间,消息只有false和true。设false是− 1 / 8 ( − 1 / 8 = 7 / 8 ) ,噪声小于1 / 16,设true是1/8,噪声也小于1 / 16 
然后我们把两个环面相加。它们的值可能是真或假。如果他们都是假,那会得到3 / 4(红色),如果他们一真一假,会得0(黄色),如果他们都是真,得到1 / 4(绿色)。: 
在能够看到明文的条件下,如何进行自举的与非操作呢?非常简单,我们把这个环面画一条线,落在线的左边就输出true,落在右边就输出false:

难点在于我们如何在密文下进行操作。TFHE给出了这样的答案:
盲旋转


1.首先将环面分为 2 N个部分,想象成图中的轮子,上面带有 2 N个槽。 2.然后将要返回的 2 N个值放入槽中,完成设置 (Setup) 步骤。 3.进行明文旋转 (PlainRotate) 过程,该过程进行旋转的人可以知道具体旋转了多少个位置。 4.进行密文旋转 (EncRotate) 过程,该过程进行旋转的人不知道旋转了多少个位置,并且得到的是加5.密的密文,无法通过旋转前后判断旋转了多少位置。可以理解为放在一个黑盒中进行了一波操作。 6.最终将 0 位置的密文取出,即为所需要的结果。
